Линейные операции над векторами в координатной форме. Условие коллинеарности двух векторов. Деление отрезка в данном отношении и, в частности, пополам.
Date: 2015-10-07; view: 437.
Линейные операции над векторами в координатной форме:
a={X1,Y1,Z1}, b={X2,Y2,Z2}.
1) Сложение.
a+ b={X1 + X2; Y1 + Y2; Z1+ Z2};
2) Разность.
a- b={X1 - X2; Y1 - Y2; Z1- Z2};
3) Умножение.
α*a={α*X1; α*Y1; α*Z1};
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов a={X1,Y1,Z1} и b={X2,Y2,Z2} является пропорциональность координат:
Рассмотрим в пространстве две различные точки 
и 
и прямую, определяемую этими точками. Выберем на этой прямой некоторое направление. На полученной оси точки M1 и M2 определяют направленный отрезок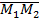 
. Пусть М — любая отличная от точка указанной выше оси. Число λ= 
называется отношением, в котором точка M делит направленный отрезок 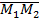. Таким образом, любая, отличная от M2
точка M делит отрезок 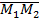в некотором отношении λ, где λ определяется равенством λ= 
.
Согласно М1М2 = х2-х1, получаем М1M = x — x1, a MМ2 = x2— х, следовательно λ= 
=> x= 
Совершенно аналогично вычисляются координаты y и z точки M.
Таким образом: x= , y= 
, z= 
.
Эти формулы называются формулами деления отрезка в данном отношении λ.
Очевидно, если λ=1, то точка М делит отрезок 
пополам. Получающиеся формулы (из соотношений x= , y= , z= ) называются формулами деления отрезка пополам.
x=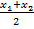 
, y= 
, z= 
.