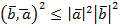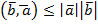Скалярное произведение двух векторов. Его определение через взаимные прямоугольные проекции. Неравенство Коши.
Date: 2015-10-07; view: 458.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение векторов a и b будем обозначать символом ab. Если угол между векторами a и b равен ϕ, то по определению скалярное произведение этих двух векторов выражается формулой
ab = |a||b|cosϕ.
Т.к. проекция вектора b на ось u равна длине вектора b, умноженной на косинус ϕ угла наклона вектора b
к оси u, то ab = |a||b|cosϕ = |a|прba
Скалярным произведением двух векторов называется число, равное произведению длины одного
из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.
Неравенство Коши.

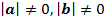
Рассмотрим вектор (xb-a)2