Векторное произведение векторов и его свойства

Date: 2015-10-07; view: 509.

Определение скалярного произведения векторов и его свойства.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается ab,а* b(или( а, b))

Свойства:

1. Скалярное произведение обладает переместительным свойством: ab=ba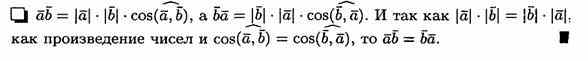

Векторным произведением двух векторов А и В называется вектор , перпендикулярный данным и численно равен скалярному произведению этих векторов на sin угла между ними. Полученный вектор дополняет данные до правой тройки векторов.

Свойства:

1) Векторное произведение 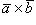равно нулю, если векторы 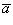и 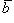коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

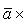
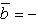
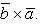
Векторное произведение не обладает свойством переместительности.