Смешанным произведением векторов. Свойства.

Date: 2015-10-07; view: 344.

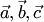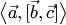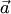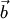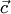Смешанным произведением векторов называется число , равное скалярному произведению вектора на векторное произведение векторов и . Смешанное произведение обозначается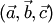

Свойства смешанного произведения:

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b .

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер

2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).

Действительно, (ахb )•с=±V и а•(b хс)=(b хс)•а=±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации.

Следовательно, (a хb )•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b )с в виде abc без знаков векторного, скалярного умножения.

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .

Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4.Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны.

Если abc =0 , то а, b и с— компланарны.