Прямая на плоскости. Способы задания прямой на плоскости.

Date: 2015-10-07; view: 491.

Замена базиса и системы координат. Изменение координат вектора при параллельном переносе.

Общее уравнение прямой линии на плоскости в декартовых координатах:

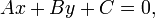
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

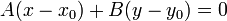
Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке 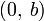и образующая угол 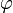с положительным направлением оси Ox:

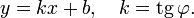
Коэффициент k называется

угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.

Уравнение прямой в отрезках. Прямая линия, пересекающая ось Ox в точке 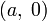и ось Oy в точке :

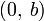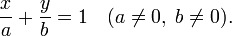
В этом виде невозможно представить прямую, проходящую через начало координат.