
Нормальное (нормированное) уравнение плоскости
Date: 2015-10-07; view: 424.
Уравение плоскости. Способы задания плоскости.(-по точке и нормальному вектору –общее уравнение плосоксти -уравение плоскости, проходящей через три заданные точки –нормально уравнение плоскости –в отрезках)
Нормальное уравнение прямой
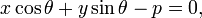
где p — длина перпендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
Уравнение плоскости в отрезках:
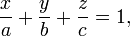
где 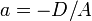 ,
, 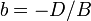 ,
, 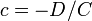 — отрезки, отсекаемые плоскостью на осях
— отрезки, отсекаемые плоскостью на осях 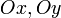 и
и 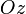 .
.
Уравнение плоскости, проходящей через точку 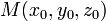 перпендикулярно вектору нормали
перпендикулярно вектору нормали 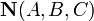 :
:
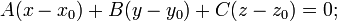
в векторной форме:
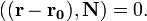
Уравнение плоскости, проходящей через три заданные точки 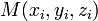 , не лежащие на одной прямой:
, не лежащие на одной прямой:
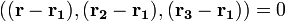
(смешанное произведение векторов), иначе
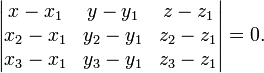
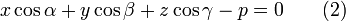
| <== previous lecture | | | next lecture ==> |
| Прямая на плоскости. Способы задания прямой на плоскости. | | | Угол между двумя прямыми в пространстве. Угол между прямой и плоскостью. |