Теорема Коши. Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента

Теорема Лагранжа

Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то 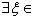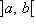такое, что f(b) - f(a) = f'(ξ)(b - a).

Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производная g'(x) ≠ 0 на ]a, b[, то 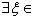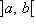такое, что справедлива формула

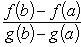
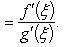
Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким:

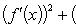
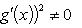
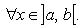
9. Правило Лопиталя.Это правило нахождения некоторых пределов функций при помощи производных. Правило Лопиталя задается следующей теоремой.

Теорема 2. Пусть 1) функции f (x) и g(x) дифференцируемы в некоторой проколотой окрестности* точки а, 2) 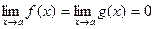(или ¥), 3) g(x) ¹ 0 и g’(x) ¹ 0 в этой окрестности. Тогда, если существует 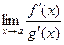, то существует и верно равенство

.

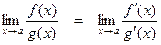Замечание 4. Теорема верна и для случая а = ¥ (+¥, – ¥).

Замечание 5. Теорема верна и для случая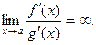

Замечание 6. Из условий теоремы следует, что функция 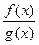является неопределенностью вида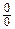 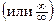при 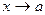, следовательно, теорема позволяет в некоторых случаях раскрыть эти неопределенности.

Замечание 7. Часто правило Лопиталя применяется повторно следующим образом. Пусть при выполнении условий 1) – 3) теоремы 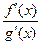является неопределенностью вида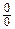 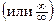. Тогда правило Лопиталя применяется повторно к 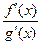и т. д. Если после нескольких повторных применений правила будет получено конечное или бесконечное значение, то оно будет равно .

Примеры.9) Найти предел

Решение. Функции f (x) = e^x – e^-x и g(x) = ln(1+x) удовлетворяют условиям 1) – 3) теоремы 2, причем имеет место неопределенность вида 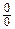. Применим правило Лопиталя:

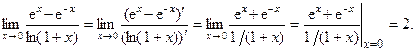
10) Найти предел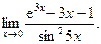

Решение. Имеет место неопределенность вида 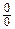. Применим правило Лопиталя.

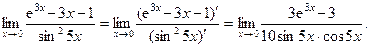
Вновь имеет место неопределенность вида 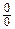. Следуя замечанию 7, применим правило Лопиталя повторно. При этом замечаем, что 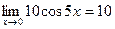, поэтому правило применяем только к функции :

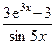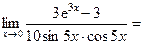
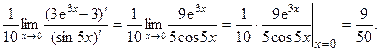
11) Найти предел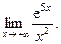

Решение. Имеет место неопределенность вида 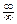. Применим правило Лопиталя.

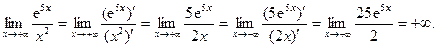
Здесь правило Лопиталя применено два раза.

Замечание 8. Результат будет таким же и при любом положительном коэффициенте у показателя экспоненты и любом положительном показателе степени х. Этот факт неформально означает, что “экспоненциальная функция растет быстрее, чем степенная при х ® + ¥”.

12) Найти предел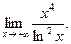

Решение. Имеет место неопределенность вида 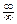. Применим правило Лопиталя.

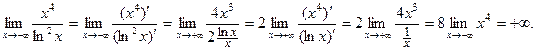
Здесь правило Лопиталя применено два раза.

Замечание 9. Результат будет таким же и при любых положительных показателях степеней х и lnx. Этот факт неформально означает, что “степенная функция растет быстрее, чем логарифмическая при х ®+¥”.

Дата добавления: 2014-02-28; просмотров: 519; Нарушение авторских прав

Мы поможем в написании ваших работ!