
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Интегральное исчисление функций многих переменных и элементы векторного анализа
Пусть 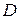 некоторая замкнутая ограниченная область, а
некоторая замкнутая ограниченная область, а 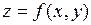 произвольная функция, определенная и ограниченная в этой области. Потребуем также, чтобы граница этой области была кусочно-непрерывной, то есть состояла из конечного числа кривых вида
произвольная функция, определенная и ограниченная в этой области. Потребуем также, чтобы граница этой области была кусочно-непрерывной, то есть состояла из конечного числа кривых вида 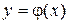 или
или 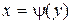 , где
, где 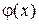 и
и 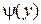 непрерывные функции.
непрерывные функции.
Разобьем область 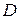 произвольно на
произвольно на 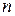 частей
частей 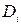 (
(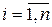 ), таких что
), таких что 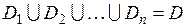 и
и 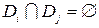 ,
, 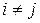 . Обозначим
. Обозначим 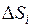 площадь
площадь 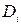 (
(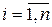 ). В каждой области
). В каждой области 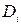 выберем произвольно точку
выберем произвольно точку 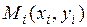 и составим сумму
и составим сумму
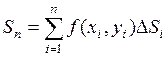 .
.
Сумма 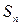 называется интегральной суммой для функции
называется интегральной суммой для функции 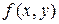 в области
в области 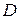 .
.
Диаметром 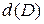 области
области 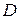 называется наибольшее расстояние между граничными точками этой области. Обозначим
называется наибольшее расстояние между граничными точками этой области. Обозначим 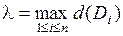 .
.
Если существует предел интегральной суммы 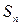 при
при 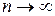 и
и 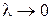 , не зависящий ни от способа разбиения области
, не зависящий ни от способа разбиения области 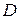 на части
на части 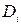 , ни от выбора точек
, ни от выбора точек 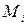 , то этот предел называется двойным интегралом от функции
, то этот предел называется двойным интегралом от функции 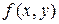 по области
по области 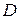 , и обозначается
, и обозначается
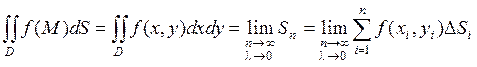 .
.
Функция  при этом называется подынтегральной функцией,
при этом называется подынтегральной функцией,  – областью интегрирования,
– областью интегрирования, 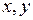 – переменными интегрирования,
– переменными интегрирования, 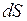 (или
(или 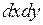 ) – элементом площади. Функция
) – элементом площади. Функция 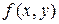 , для которой в области
, для которой в области 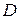 существует двойной интеграл, называется интегрируемой в области
существует двойной интеграл, называется интегрируемой в области 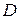 .
.
Область 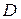 называется правильной или элементарной по отношению к оси
называется правильной или элементарной по отношению к оси 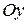 (
(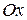 ), если прямая, параллельная оси
), если прямая, параллельная оси 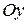 (
(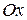 ) и проходящая через любую внутреннюю точку области
) и проходящая через любую внутреннюю точку области 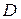 , пересекает границу
, пересекает границу 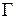 этой области не более, чем в двух точках.
этой области не более, чем в двух точках.
Пусть функция 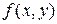 интегрируема на правильной по отношению к оси
интегрируема на правильной по отношению к оси 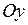 области
области 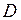 , ограниченной прямыми
, ограниченной прямыми 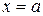 ,
, 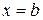 и графиками функций
и графиками функций 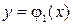 и
и 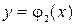 , причем
, причем 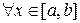
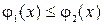 . Тогда двойной интеграл от функции
. Тогда двойной интеграл от функции 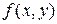 по данной области
по данной области 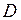 равен
равен
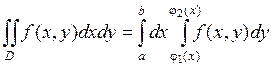 .
.
Геометрический смысл двойного интеграла заключается в том, что если 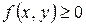 в области
в области 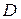 , то двойной интеграл численно равен объёму
, то двойной интеграл численно равен объёму 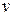 криволинейного цилиндра, ограниченного сверху поверхностью
криволинейного цилиндра, ограниченного сверху поверхностью 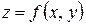 , снизу плоскостью
, снизу плоскостью 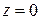 и сбоку цилиндрической поверхностью с направляющей
и сбоку цилиндрической поверхностью с направляющей 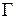 и образующими, параллельными оси
и образующими, параллельными оси 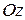 , вырезающей на плоскости
, вырезающей на плоскости 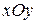 область
область 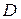 , то есть
, то есть 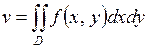 .
.
Пусть 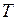 некоторая замкнутая ограниченная область в
некоторая замкнутая ограниченная область в 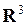 , а
, а 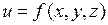 произвольная функция, определенная и ограниченная в этой области.
произвольная функция, определенная и ограниченная в этой области.
Разобьем область 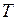 произвольно на
произвольно на  частей
частей 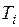 (
(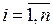 ), таких что
), таких что 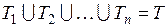 и
и 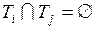 ,
, 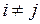 . Обозначим
. Обозначим 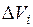 объем
объем 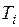 (
(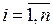 ). В каждой области
). В каждой области 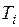 выберем произвольно точку
выберем произвольно точку  и составим сумму
и составим сумму
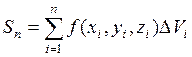 .
.
Сумма 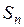 называется интегральной суммой для функции
называется интегральной суммой для функции 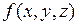 в области
в области 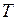 . Обозначим
. Обозначим 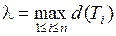 .
.
Если существует предел интегральной суммы 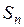 при
при 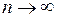 и
и 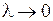 , не зависящий ни от способа разбиения области
, не зависящий ни от способа разбиения области 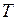 на части
на части 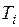 , ни от выбора точек
, ни от выбора точек 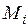 , то этот предел называется тройным интегралом от функции
, то этот предел называется тройным интегралом от функции 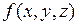 по области
по области 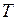 , и обозначается
, и обозначается
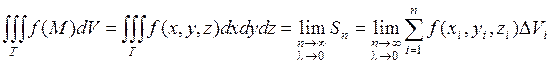 .
.
Функция 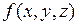 при этом называется подынтегральной функцией,
при этом называется подынтегральной функцией, 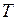 – областью интегрирования,
– областью интегрирования, 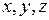 – переменными интегрирования,
– переменными интегрирования, 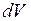 (или
(или 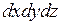 ) – элементом объема. Функция
) – элементом объема. Функция 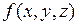 , для которой в области
, для которой в области 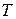 существует тройной интеграл, называется интегрируемой в области
существует тройной интеграл, называется интегрируемой в области 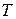 .
.
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению одного однократного и одного двойного интегралов или к вычислению трех однократных интегралов.
Область 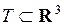 называется правильной или элементарной по отношению к оси
называется правильной или элементарной по отношению к оси 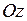 (
(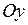 или
или 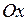 ), если прямая, параллельная оси
), если прямая, параллельная оси 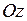 (
(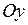 или
или 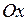 ) и проходящая через любую внутреннюю точку области
) и проходящая через любую внутреннюю точку области 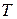 , пересекает границу
, пересекает границу 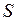 этой области не более, чем в двух точках. Область
этой области не более, чем в двух точках. Область 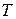 называется простой, если её можно разбить на конечное число элементарных областей.
называется простой, если её можно разбить на конечное число элементарных областей.
Пусть функция 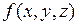 непрерывна в правильной по отношению к оси
непрерывна в правильной по отношению к оси 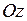 области
области 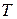 , ограниченной снизу и сверху поверхностями
, ограниченной снизу и сверху поверхностями 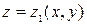 и
и 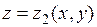 , причем
, причем 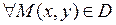
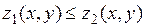 , и ограничена с боков прямым цилиндром, сечением которого плоскостью, параллельной плоскости
, и ограничена с боков прямым цилиндром, сечением которого плоскостью, параллельной плоскости 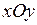 , является область
, является область 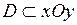 . Тогда тройной интеграл от функции
. Тогда тройной интеграл от функции 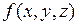 по данной области
по данной области 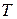 равен
равен
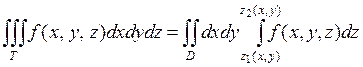 .
.
Если правильная область 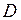 , ограничена прямыми
, ограничена прямыми 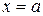 ,
, 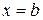 и графиками функций
и графиками функций 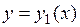 и
и 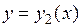 , причем
, причем 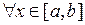
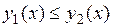 , то тройной интеграл от функции
, то тройной интеграл от функции 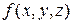 по области
по области 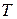 равен
равен
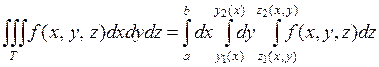 .
.
Пусть на спрямляемой (имеющей конечную длину) простой кривой 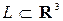 с началом в точке
с началом в точке  и концом в точке
и концом в точке 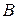 задана непрерывная функция
задана непрерывная функция 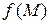 ,
, 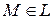 . Разобьем кривую
. Разобьем кривую 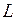 на
на  частей точками
частей точками 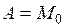 ,
, 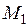 ,
, 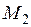 ,
, 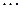 ,
, 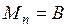 , причем так, чтобы
, причем так, чтобы 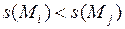 при
при 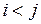 , где функция
, где функция 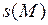 определяет длину дуги
определяет длину дуги 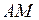 кривой
кривой 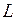 . Такое разбиение
. Такое разбиение 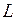 задает ориентацию кривой, то есть определяет направление движения вдоль кривой от точки
задает ориентацию кривой, то есть определяет направление движения вдоль кривой от точки 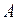 к точке
к точке 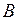 .
.
Выберем на каждой дуге 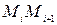 произвольную точку
произвольную точку 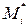 и составим интегральную сумму
и составим интегральную сумму
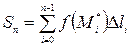 ,
,
где 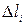 – длина дуги
– длина дуги 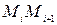 ,
, 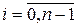 . Пусть
. Пусть 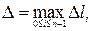 .
.
Если существует предел
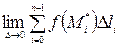 ,
,
не зависящий ни от способа деления дуги 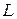 на части
на части 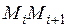 , ни от выбора точек
, ни от выбора точек 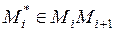 , то этот предел называется криволинейным интегралом первого рода по дуге
, то этот предел называется криволинейным интегралом первого рода по дуге 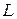 от функции
от функции 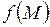 и обозначается
и обозначается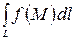 .
.
Таким образом, по определению,
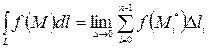 .
.
Пусть 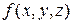 – непрерывная функция, а
– непрерывная функция, а 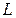 – гладкая кривая, заданная параметрическими уравнениями
– гладкая кривая, заданная параметрическими уравнениями 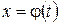 ,
, 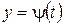 ,
, 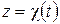 ,
, 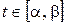 ,
, 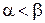 , причем для начала
, причем для начала 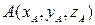 и конца
и конца 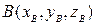 кривой выполняются соотношения
кривой выполняются соотношения 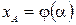 ,
, 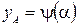 ,
, 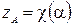 ,
, 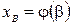 ,
, 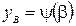 ,
, 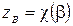 . Тогда
. Тогда
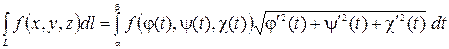 .
.
Иногда кривую 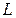 можно параметризовать, выбирая в качестве параметра
можно параметризовать, выбирая в качестве параметра 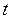 одну из прямоугольных декартовых координат
одну из прямоугольных декартовых координат 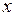 ,
, 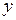 или
или 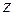 . Например, пусть кривая
. Например, пусть кривая 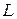 задана на плоскости графиком функции
задана на плоскости графиком функции 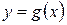 ,
, 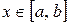 , то есть
, то есть 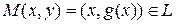 , и пусть
, и пусть 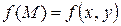 – непрерывная функция на
– непрерывная функция на 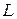 . Параметризуем кривую, полагая
. Параметризуем кривую, полагая 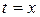 . Тогда
. Тогда 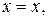
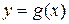 и
и
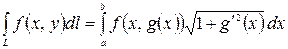 .
.
Пусть на простой кривой 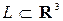 с началом в точке
с началом в точке 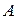 и концом в точке
и концом в точке 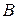 задана некоторая функция
задана некоторая функция 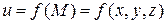 . Разобьем кривую
. Разобьем кривую 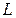 точками
точками 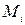 на
на 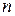 частей
частей 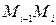 (длина каждой
(длина каждой 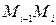 равна
равна 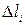 ). На каждой дуге
). На каждой дуге 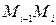 выберем точку
выберем точку 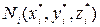 и составим интегральную сумму
и составим интегральную сумму
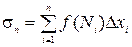 ,
,
где  – проекция дуги
– проекция дуги 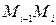 на ось
на ось 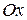 (то есть
(то есть 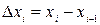 , а
, а 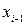 ,
, 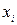 – абсциссы точек
– абсциссы точек 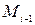 и
и 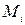 , соответственно). Обозначим
, соответственно). Обозначим 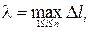 .
.
Если существует предел интегральной суммы 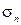 при
при 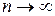 и
и 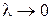 , не зависящий ни от способа разбиения кривой
, не зависящий ни от способа разбиения кривой 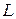 на части
на части 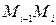 , ни от выбора точек
, ни от выбора точек 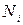 , то этот предел называется криволинейным интегралом второго рода по координате
, то этот предел называется криволинейным интегралом второго рода по координате 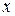 от функции
от функции 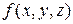 по кривой
по кривой 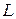 , и обозначается
, и обозначается
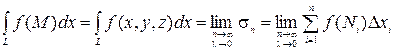 .
.
Аналогично определяются криволинейные интегралы второго рода по координатам 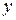 и
и 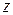 . Рассмотрим общий случай.
. Рассмотрим общий случай.
Пусть на простой кривой 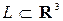 заданы функции
заданы функции 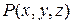 ,
, 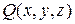 ,
, 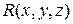 . Проведем разбиение кривой
. Проведем разбиение кривой 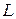 как в предыдущем случае и составим интегральную сумму
как в предыдущем случае и составим интегральную сумму
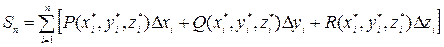 ,
,
где  ,
, 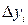 ,
, 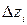 – проекции дуги
– проекции дуги 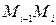 на оси
на оси 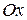 ,
, 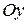 ,
, 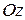 , соответственно. Пусть
, соответственно. Пусть 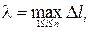 .
.
Если существует предел интегральной суммы 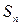 при
при 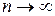 и
и 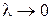 , не зависящий ни от способа разбиения кривой
, не зависящий ни от способа разбиения кривой 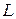 на части
на части 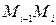 , ни от выбора точек
, ни от выбора точек 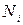 , то этот предел называется криволинейным интегралом второго рода (общего вида) от функций
, то этот предел называется криволинейным интегралом второго рода (общего вида) от функций 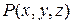 ,
, 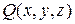 ,
, 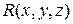 по кривой
по кривой 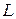 , и обозначается
, и обозначается
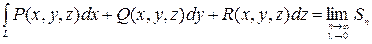 .
.
Следует заметить, что криволинейный интеграл второго рода также как и криволинейный интеграл первого рода обладает свойствами линейности и аддитивности, однако для интегралов второго рода при изменении направления интегрирования меняется знак интеграла. Если кривая интегрирования 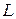 является замкнутой кривой, то криволинейный интеграл второго рода по этой кривой обозначается
является замкнутой кривой, то криволинейный интеграл второго рода по этой кривой обозначается
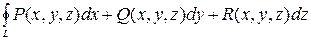 .
.
Пусть 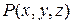 ,
, 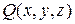 ,
, 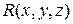 – непрерывные функции, а
– непрерывные функции, а 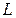 – гладкая кривая, заданная параметрическими уравнениями
– гладкая кривая, заданная параметрическими уравнениями 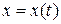 ,
, 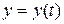 ,
, 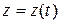 ,
, 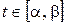 ,
, 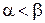 , причем для начала
, причем для начала 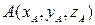 и конца
и конца 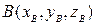 кривой выполняются соотношения
кривой выполняются соотношения 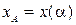 ,
, 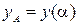 ,
, 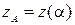 ,
, 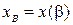 ,
, 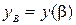 ,
, 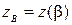 . Тогда
. Тогда
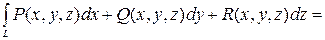
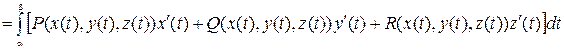 .
.
Говорят, что граница 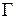 области
области 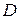 ориентирована положительно (отрицательно),если при движении по
ориентирована положительно (отрицательно),если при движении по 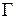 область
область 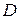 располагается с левой (правой) стороны. При этом говорят, что область D ориентирована положительно (отрицательно), если ее граница
располагается с левой (правой) стороны. При этом говорят, что область D ориентирована положительно (отрицательно), если ее граница 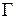 ориентирована положительно (отрицательно).
ориентирована положительно (отрицательно).
Пусть функции 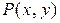 и
и 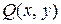 и их частные производные
и их частные производные 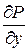 и
и 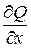 непрерывны в замкнутой области
непрерывны в замкнутой области 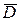 (односвязной или многосвязной), ограниченной кусочно-гладкой кривой
(односвязной или многосвязной), ограниченной кусочно-гладкой кривой 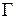 . Тогда справедливо равенство
. Тогда справедливо равенство
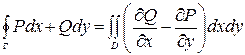 ,
,
где криволинейный интеграл вычисляется по границе 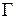 области
области 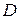 , ориентированной положительно. Это равенство называется формулой Грина. Формула Грина связывает криволинейный интеграл второго рода по замкнутой кривой с двойным интегралом по области, ограниченной этой кривой.
, ориентированной положительно. Это равенство называется формулой Грина. Формула Грина связывает криволинейный интеграл второго рода по замкнутой кривой с двойным интегралом по области, ограниченной этой кривой.
Пусть в пространстве  на кусочно-гладкой поверхности
на кусочно-гладкой поверхности 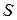 задана непрерывная функция
задана непрерывная функция 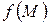 . Разобьём поверхность
. Разобьём поверхность 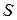 кусочно-гладкими линиями на части
кусочно-гладкими линиями на части 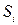 с соответствующими площадями
с соответствующими площадями 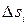 ,
, 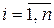 . В каждой части
. В каждой части 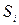 произвольно выберем точку
произвольно выберем точку 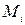 и составим интегральную сумму
и составим интегральную сумму
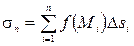 .
.
Обозначим 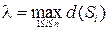 максимальный из диаметров частей
максимальный из диаметров частей 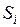 .
.
Если существует предел интегральной суммы 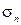 при
при 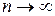 и
и 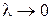 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности 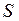 на части
на части 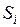 , ни от выбора точек
, ни от выбора точек 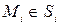 ,
, 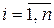 , то он называется поверхностным интегралом первого рода от функции
, то он называется поверхностным интегралом первого рода от функции 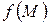 по поверхности
по поверхности  , и обозначается
, и обозначается 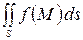 .
.
Если поверхность  задана явно уравнением
задана явно уравнением 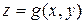 ,
, 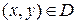 то поверхностный интеграл первого рода от функции
то поверхностный интеграл первого рода от функции 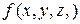 по поверхности
по поверхности  равен
равен
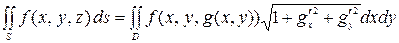 .
.
Пусть в пространстве 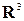 задана некоторая гладкая поверхность
задана некоторая гладкая поверхность  . В каждой точке такой поверхности существует вектор нормали
. В каждой точке такой поверхности существует вектор нормали 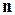 . Пусть
. Пусть 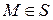 некоторая внутренняя точка поверхности
некоторая внутренняя точка поверхности  , а
, а 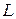 некоторая замкнутая кривая, целиком лежащая на поверхности
некоторая замкнутая кривая, целиком лежащая на поверхности  и проходящая только через внутренние точки поверхности
и проходящая только через внутренние точки поверхности  , кроме того
, кроме того 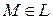 . Выберем направление вектора
. Выберем направление вектора 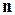 в точке
в точке 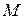 .
.
Гладкая поверхность  называется двусторонней, если для любых точки
называется двусторонней, если для любых точки 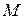 и кривой
и кривой 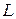 вектор нормали
вектор нормали 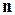 после обхода кривой
после обхода кривой 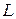 при возвращении в исходную точку
при возвращении в исходную точку 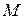 имеет первоначально выбранное направление. В противном случае гладкая поверхность называется односторонней.
имеет первоначально выбранное направление. В противном случае гладкая поверхность называется односторонней.
Пусть на двусторонней поверхности  выбрана одна сторона, тогда говорят, что поверхность
выбрана одна сторона, тогда говорят, что поверхность  ориентирована. Ориентацию поверхности задают выбором в точках этой поверхности направления вектора нормали
ориентирована. Ориентацию поверхности задают выбором в точках этой поверхности направления вектора нормали 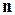 в выбранную сторону.
в выбранную сторону.
Пусть в точках ориентированной поверхности  задана функция
задана функция 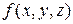 . Разобьем
. Разобьем  кусочно-гадкими кривыми на куски
кусочно-гадкими кривыми на куски 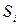 ,
, 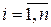 . В пределах каждого куска выберем произвольно точку
. В пределах каждого куска выберем произвольно точку 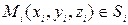 и составим интегральную сумму
и составим интегральную сумму
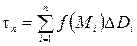 ,
,
где 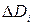 – величина, равная площади проекции ориентированной поверхности
– величина, равная площади проекции ориентированной поверхности 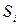 на плоскость
на плоскость 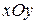 , взятая со знаком плюс, если
, взятая со знаком плюс, если 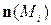 и ось
и ось 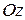 образуют острый угол, и минус, если этот угол тупой. Обозначим
образуют острый угол, и минус, если этот угол тупой. Обозначим 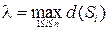 .
.
Если существует предел интегральной суммы 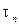 при
при 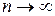 и
и 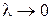 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности 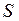 на части
на части 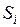 , ни от выбора точек
, ни от выбора точек 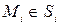 ,
, 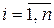 , то он называется поверхностным интегралом второго рода по переменным
, то он называется поверхностным интегралом второго рода по переменным 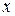 и
и 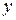 от функции
от функции 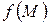 по ориентированной поверхности
по ориентированной поверхности  , и обозначается
, и обозначается 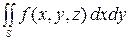 .
.
Аналогично определяются поверхностные интегралы второго рода по переменным 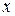 ,
, 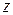 и
и 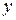 ,
, 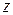 . Рассмотрим общий случай.
. Рассмотрим общий случай.
Пусть на ориентированной поверхности 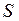 заданы функции
заданы функции 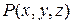 ,
, 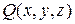 ,
, 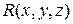 . Как в предыдущем случае проведем разбиение поверхности
. Как в предыдущем случае проведем разбиение поверхности 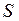 и составим интегральную сумму
и составим интегральную сумму
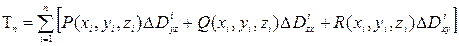 ,
,
где 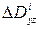 ,
, 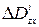 ,
, 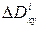 – площади проекции поверхности
– площади проекции поверхности 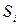 на плоскости
на плоскости 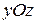 ,
, 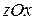 ,
, 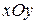 , взятые со знаком плюс или минус, в зависимости от того составляет ли острый (тогда «+») или тупой (тогда «–») угол вектор
, взятые со знаком плюс или минус, в зависимости от того составляет ли острый (тогда «+») или тупой (тогда «–») угол вектор 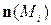 и осями
и осями 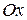 ,
, 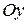 ,
, 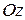 . Обозначим
. Обозначим 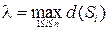 .
.
Если существует предел интегральной суммы 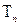 при
при 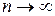 и
и 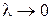 , не зависящий ни от способа разбиения поверхности
, не зависящий ни от способа разбиения поверхности 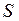 на части
на части 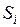 , ни от выбора точек
, ни от выбора точек 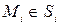 ,
, 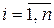 , то он называется поверхностным интегралом второго рода (общего вида) от функций
, то он называется поверхностным интегралом второго рода (общего вида) от функций 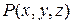 ,
, 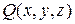 ,
, 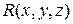 по ориентированной поверхности
по ориентированной поверхности  , и обозначается
, и обозначается
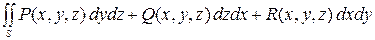 .
.
Если 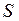 – замкнутая поверхность, то поверхностный интеграл второго рода обозначается
– замкнутая поверхность, то поверхностный интеграл второго рода обозначается
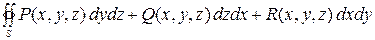 .
.
Пусть поверхность 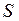 однозначно проектируется на координатные плоскости
однозначно проектируется на координатные плоскости 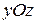 ,
, 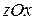 ,
, 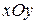 в области
в области 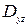 ,
, 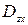 ,
, 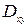 . В этом случае возможно явное задание поверхности
. В этом случае возможно явное задание поверхности 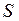 с помощью уравнений
с помощью уравнений
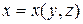 ,
, 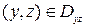 ;
; 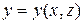 ,
, 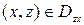 ,
, 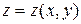 ,
, 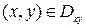 .
.
Тогда поверхностный интеграл второго рода от функций 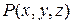 ,
, 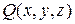 ,
, 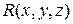 по ориентированной поверхности
по ориентированной поверхности  равен
равен
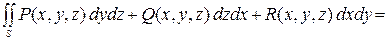
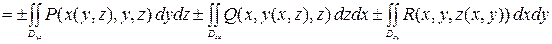 ,
,
где знак перед первым интегралом выбирается плюс, если 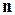 и ось
и ось 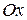 образуют острый угол (минус – если угол тупой); знак перед вторым интегралом выбирается плюс, если
образуют острый угол (минус – если угол тупой); знак перед вторым интегралом выбирается плюс, если 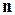 и ось
и ось 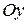 образуют острый угол (минус – если угол тупой); знак перед третьим интегралом выбирается плюс, если
образуют острый угол (минус – если угол тупой); знак перед третьим интегралом выбирается плюс, если 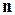 и ось
и ось 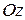 образуют острый угол (минус – если угол тупой).
образуют острый угол (минус – если угол тупой).
Формула Остроградского-Гаусса устанавливает связь между поверхностным интегралом по внешней стороне замкнутой поверхности  и тройным интегралом по пространственной области
и тройным интегралом по пространственной области 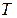 , ограниченной этой поверхностью.
, ограниченной этой поверхностью.
Пусть 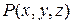 ,
, 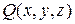 ,
, 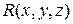 – непрерывно дифференцируемые функции в замкнутой области
– непрерывно дифференцируемые функции в замкнутой области  , ограниченной кусочно-гладкой поверхностью
, ограниченной кусочно-гладкой поверхностью  . Тогда справедлива формула Остроградского-Гаусса
. Тогда справедлива формула Остроградского-Гаусса
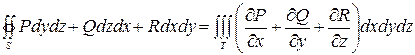 ,
,
где поверхностный интеграл берется по замкнутой поверхности  , ориентированной внешней нормалью.
, ориентированной внешней нормалью.
Формула Стокса связывает криволинейный интеграл второго рода по замкнутому контуру 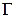 с поверхностным интегралом второго рода по поверхности
с поверхностным интегралом второго рода по поверхности  , ограниченной этим контуром.
, ограниченной этим контуром.
Пусть в области 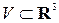 определены непрерывно дифференцируемые функции
определены непрерывно дифференцируемые функции 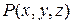 ,
, 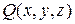 ,
, 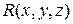 , и в этой области расположена положительно ориентированная гладкая поверхность
, и в этой области расположена положительно ориентированная гладкая поверхность  , ограниченная кусочно-гладким контуром
, ограниченная кусочно-гладким контуром 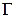 . Тогда справедлива формула Стокса
. Тогда справедлива формула Стокса
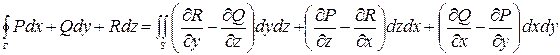 .
.
Закон, по которому каждой точке 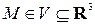 поставлено в соответствие некоторое число
поставлено в соответствие некоторое число 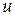 , называется скалярным полем, и обозначается
, называется скалярным полем, и обозначается 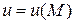 . Другими словами, скалярное поле – есть некоторая скалярная функция нескольких переменных
. Другими словами, скалярное поле – есть некоторая скалярная функция нескольких переменных 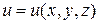 ,
, 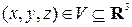 . Если скалярное поле задано функцией двух переменных
. Если скалярное поле задано функцией двух переменных 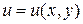 , то оно называется плоским.
, то оно называется плоским.
Геометрической характеристикой скалярного поля служат поверхности уровня (для плоского скалярного поля – линии уровня). Поверхность уровня – это множество точек пространства, в которых значение скалярного поля постоянно, то есть 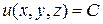 (для линий уровня
(для линий уровня 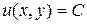 ).
).
Пусть в некоторой области евклидова пространства 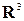 задано скалярное поле
задано скалярное поле 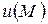 . Рассмотрим это поле в прямоугольной декартовой системе координат
. Рассмотрим это поле в прямоугольной декартовой системе координат 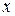 ,
, 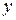 ,
, 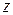 и зафиксируем точку
и зафиксируем точку 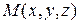 . Проведем через эту точку прямую в направлении вектора
. Проведем через эту точку прямую в направлении вектора 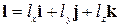 с началом в точке
с началом в точке 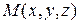 и рассмотрим значения скалярной функции
и рассмотрим значения скалярной функции 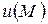 в точке
в точке 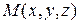 и в близких к ней точках
и в близких к ней точках 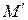 . Введем число
. Введем число 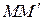 , равное длине вектора
, равное длине вектора 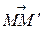 (
(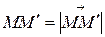 ), если векторы
), если векторы 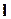 и
и 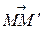 совпадают по направлению, и равное
совпадают по направлению, и равное 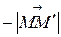 , если эти векторы противоположны по направлению.
, если эти векторы противоположны по направлению.
Производной скалярной функции 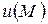 в точке
в точке 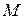 по направлению вектора
по направлению вектора 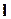 называется предел
называется предел 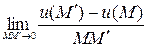 , обозначаемый символом
, обозначаемый символом 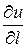 .
.
Их этого определения следует, что производная скалярной функции по заданному направлению является скаляром. Рассмотрим приращение 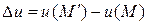 . Для этого введем обозначение
. Для этого введем обозначение 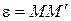 и единичный вектор
и единичный вектор 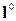 по направлению
по направлению 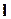 :
:
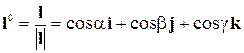 ,
,
где 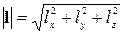 ;
; 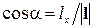 ,
, 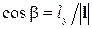 ,
, 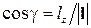 – соответствующие проекции вектора
– соответствующие проекции вектора 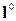 на оси
на оси 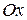 ,
, 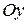 ,
, 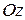 . Тогда
. Тогда
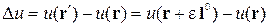 ,
,
где 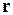 и
и 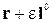 – радиус-векторы точек
– радиус-векторы точек 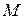 и
и 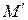 соответственно. В прямоугольных декартовых координатах приращение
соответственно. В прямоугольных декартовых координатах приращение 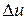 примет вид
примет вид
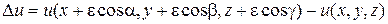 .
.
Таким образом, приращение 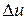 можно рассматривать как сложную функцию независимой переменной
можно рассматривать как сложную функцию независимой переменной 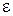 . Предполагая дифференцируемость функции
. Предполагая дифференцируемость функции 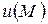 в точке
в точке 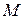 , запишем
, запишем
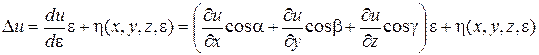 ,
,
где 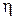 – бесконечно малая функция более высокого порядка, чем
– бесконечно малая функция более высокого порядка, чем 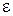 при
при 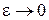 .
.
Подставляя найденное приращение 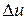 в определение производной скалярной функции по направлению, получаем
в определение производной скалярной функции по направлению, получаем
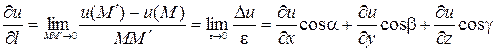 ,
,
то есть
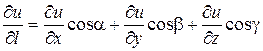 .
.
В частности, если вектор 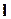 сонаправлен с одной из координатных осей, то производная по направлению
сонаправлен с одной из координатных осей, то производная по направлению 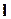 совпадает с соответствующей частной производной. Например, если
совпадает с соответствующей частной производной. Например, если 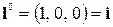 , то
, то
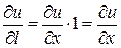 .
.
Производная поля в точке 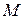 по направлению
по направлению 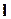 характеризует скорость изменения поля по направлению
характеризует скорость изменения поля по направлению 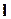 , а частные производные
, а частные производные 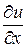 ,
, 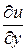 ,
, 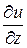 – скорость изменения скалярного поля
– скорость изменения скалярного поля 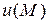 по направлению осей
по направлению осей 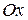 ,
, 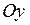 ,
, 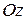 соответственно.
соответственно.
Градиентом скалярного поля 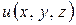 в точке
в точке 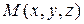 называется вектор, обозначаемый
называется вектор, обозначаемый 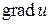 и равный
и равный
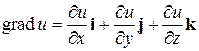 .
.
Можно показать, что 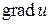 не зависит от выбора прямоугольной декартовой системы координат. С помощью градиента скалярного поля можно записать
не зависит от выбора прямоугольной декартовой системы координат. С помощью градиента скалярного поля можно записать
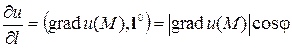 ,
,
где 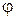 – угол между
– угол между 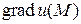 и вектором
и вектором 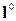 .
.
Поскольку 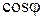 принимает максимальное значение при
принимает максимальное значение при 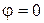 , то вектор
, то вектор 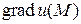 указывает направление наискорейшего возрастания функции
указывает направление наискорейшего возрастания функции 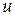 в точке
в точке 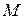 , и
, и 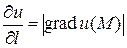 при
при 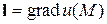 .
.
Закон, по которому каждой точке 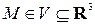 поставлен в соответствие некоторый вектор
поставлен в соответствие некоторый вектор 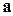 , называется векторным полем, и обозначается
, называется векторным полем, и обозначается 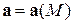 . Таким образом, векторное поле – есть некоторая векторная функция нескольких переменных, В прямоугольной декартовой системе координат
. Таким образом, векторное поле – есть некоторая векторная функция нескольких переменных, В прямоугольной декартовой системе координат 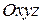 задание векторного поля
задание векторного поля 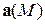 равносильно заданию трех скалярных функций
равносильно заданию трех скалярных функций 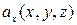 ,
, 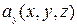 ,
, 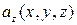
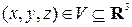 , то есть
, то есть 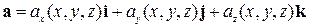 . Векторное поле вида
. Векторное поле вида 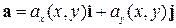 называется плоским.
называется плоским.
Геометрическими характеристиками векторного поля являются векторные линии и векторные трубки.
Кривая 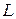 , в каждой точке
, в каждой точке 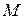 которой направление касательной совпадает с направлением вектора
которой направление касательной совпадает с направлением вектора 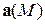 , называется векторной линией. Векторные линии определяются системой дифференциальных уравнений
, называется векторной линией. Векторные линии определяются системой дифференциальных уравнений
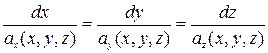 .
.
Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой не совпадающей (даже частично) с какой-либо векторной линией.
Пусть 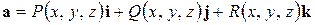 – дифференцируемое в области
– дифференцируемое в области 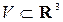 векторное поле.
векторное поле.
Скаляр, обозначаемый 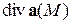 и равный
и равный
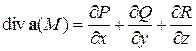 ,
,
называется дивергенцией векторного поля 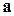 в точке
в точке 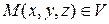 .
.
Применяя понятие дивергенции векторного поля, сформулируем теорему (формулу) Остроградского Гаусса в векторной форме.
Пусть 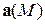 – непрерывно дифференцируемое векторное поле в замкнутой области
– непрерывно дифференцируемое векторное поле в замкнутой области 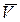 , ограниченной кусочно-гладкой поверхностью
, ограниченной кусочно-гладкой поверхностью  . Тогда справедлива формула Остроградского-Гаусса
. Тогда справедлива формула Остроградского-Гаусса
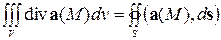 ,
,
где поток векторного поля вычисляется через замкнутую поверхность  , ориентированную внешней нормалью.
, ориентированную внешней нормалью.
Таким образом, поток векторного поля 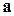 через замкнутую поверхность в сторону внешней нормали равен тройному интегралу от дивергенции векторного поля
через замкнутую поверхность в сторону внешней нормали равен тройному интегралу от дивергенции векторного поля 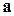 по области, ограниченной этой поверхностью.
по области, ограниченной этой поверхностью.
Из теоремы Остроградского Гаусса в векторной форме следует инвариантное определение дивергенции векторного поля.
Пусть в области 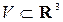 , ограниченной кусочно-гладкой поверхностью
, ограниченной кусочно-гладкой поверхностью 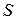 , задано непрерывно дифференцируемое векторное поле
, задано непрерывно дифференцируемое векторное поле 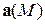 , и пусть
, и пусть 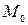 – внутренняя точка области
– внутренняя точка области 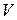 . Тогда дивергенцией векторного поля
. Тогда дивергенцией векторного поля 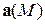 в точке
в точке 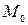 называется скаляр, обозначаемый
называется скаляр, обозначаемый 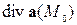 и равный
и равный
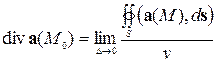 ,
,
где 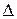 и
и 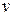 – соответственно диаметр и объем области
– соответственно диаметр и объем области 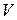 .
.
Ротором (или вихрем) векторного поля 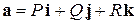 в точке
в точке 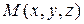 называется вектор, обозначаемый
называется вектор, обозначаемый 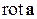 (или
(или 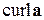 ) и равный
) и равный
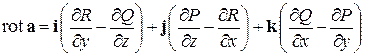 ,
,
где частные производные вычислены в этой точке.
Ротор векторного поля часто записывают в виде символического определителя
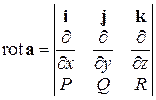 .
.
Сформулируем теорему (формулу) Стокса в векторной форме.
Пусть в области 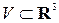 определено непрерывно дифференцируемое векторное поле
определено непрерывно дифференцируемое векторное поле 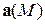 , и в этой области расположена положительно ориентированная гладкая поверхность
, и в этой области расположена положительно ориентированная гладкая поверхность  , ограниченная кусочно-гладким контуром
, ограниченная кусочно-гладким контуром 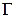 . Тогда
. Тогда
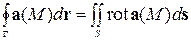 .
.
Следовательно, циркуляция векторного поля 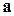 вдоль замкнутого контура равна потоку ротора поля
вдоль замкнутого контура равна потоку ротора поля 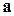 через поверхность
через поверхность 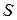 , натянутую на этот контур.
, натянутую на этот контур.
Введем поверхностный интеграл следующе
Дата добавления: 2014-02-26; просмотров: 2121; Нарушение авторских прав

Мы поможем в написании ваших работ!