Токи при размыкании цепи

Токи при размыкании и замыкании цепи

Поставим переключатель"П", рис. 3, из положения 2 в положение 1, разомкнув цепь,тогда

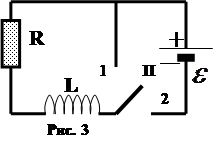IR = .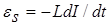

Откуда 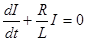(10)

Это линейное однородное дифференциальное уравнение первого порядка с разделяющимися переменными .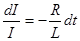

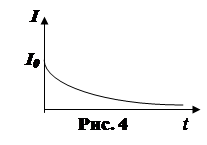Решением его будет I = 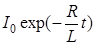, (11)

где 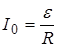. График изменения тока при размыкании цепи

представлен на рис. 4.

11.3.2. Токи при замыкании цепи

Замкнем цепь (см. рис. 3), поставив переключатель "П" в полжение 2. Для нового состояния цепи имеем в соответствии с законом Ома IR = 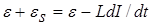. Или

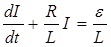(12)

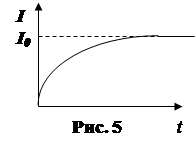Это линейное неоднородное дифференциальное уравнение первого порядка. Решением его будет 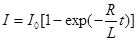(13)

где I₀=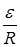, 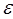- ЭДС источника, R - сопротивление нагрузки.

График изменения тока при замыкании цепи, показан на рис. 5.

11.4. Энергия магнитного поля

При возрастании тока в контуре в нем возникает ЭДС самоиндукции и закон Ома запишется 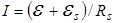, где 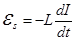, отсюда .

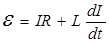Полная работа источника тока за время dt dA =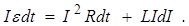

здесь I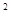Rdt - это работа, затрачиваемая на нагревание; LIdI - это работа дополнительная к работе источника тока, обусловленная индукционными явлениями в цепи. Вся работа, совершаемая в цепи для увеличения тока от 0 до I

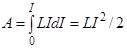. (14)

Эта работа и будет равна энергии магнитного поля, т.е. 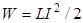. (15)

Для соленоида индуктивность L определяется по формуле (9), что позволяет найти

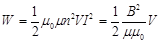. (16)

т.к. В=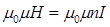. Объемная плотность энергии магнитного поля

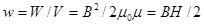, (17)

она измеряется в СИ в Дж /м³.

<== предыдущая страница	\|	следующая страница ==>
Явление самоиндукции. Явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий контур	\|	Лекция 12. Основы теории Максвелла для электромагнитного поля

Дата добавления: 2014-03-11; просмотров: 602; Нарушение авторских прав

Мы поможем в написании ваших работ!

lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.003 сек.