Лекция 12. Основы теории Максвелла для электромагнитного поля

В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса – Остроградского для электростатического поля 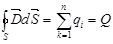и для магнитного поля 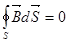; закон полного тока 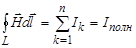; закон электромагнитной индукции 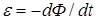, и в результате разработал законченную теорию электромагнитного поля.

Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электро­статического поля неподвижных зарядов и заканчивая электромагнитной природой света.

Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем векторного анализа – теоремы Гаусса и теоремы Стокса. Теорема Гаусса:

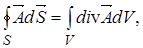(1)

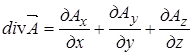(2)

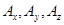- проекции вектора 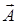на оси; V - объем, ограниченный поверхностью S.

Теорема Стокса: 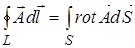. (3)

здесь rot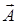- ротор вектора 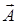, который является вектором и выражается в декартовых коор­динатах следующим образом: 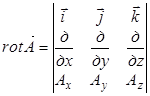, (4)

S - площадь, ограниченная контуром L.

Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.

Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.

12.1. Первое уравнение Максвелла

Оно является обобщением закона электромагнитной индукции ,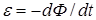

и в интегральной форме имеет следующий вид 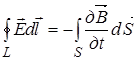(5)

и утверждает.что с переменным магнитным полем 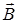неразрывно связано вихревое электри­ческое поле 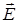, которое не зависит оттого находятся в нем проводники или нет. Из (3) следует, что 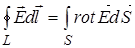. (6)

Из сравнения (5) и (6) находим, что 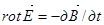(7)

Это и есть первое уравнение Максвелла в дифференциальной форме.

12.2. Ток смещения. Второе уравнение Максвелла

Максвелл обобщил закон полного тока 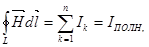предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитно­го поля. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения.

По теореме Гаусса - Остроградского поток электрического смещения сквозь замкну­тую поверхность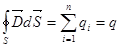

Продифференцировав это выражение по времени, получим для неподвижной и недеформирусмой поверхности S 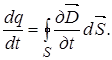(8)

Левая часть этой формулы имеет размерность тока, который, как известно, выражает­ся через вектор плотности тока 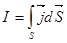. (9)

Из сравнения (8) и (9) следует, что 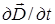имеет размерность плотности тока: А /м². Максвелл предложил назвать 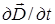плотностью тока смещения:

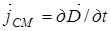. (10)

Ток смещения 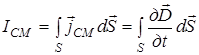. (11)

Из всех физических свойств, присущих действительному току (току проводимости), связанному с переносом зарядов, ток смещения обладает лишь одним: способностью соз­давать магнитное поле. При "протекании" тока смещения в вакууме или диэлектрике не вы­деляется тепло. Примером тока смещения может служить переменный ток через конденсатор. В общем случае токи проводимости и смещения не разделены в пространстве и мож­но говорить о полном токе, равном сумме токов проводимости и смещения: 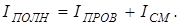(12)

С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смещения 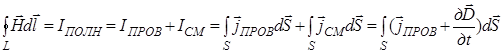. (13)

Итак, второе уравнение Максвелла в интегральной форме имеет вид:

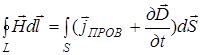. (14)

Из (3) следует, что 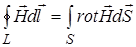. (15)

Из сравнения (14) и (15) находим, что 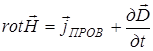. (16)

Это и есть второе уравнение Максвелла в дифференциальной форме.

12.3. Третье и четвертое уравнения Максвелла

Максвелл обобщил теорему Гаусса - Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид: 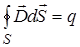. (I7) или 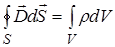. (18)

где 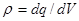- объемная плотность свободных зарядов, [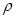]= Кл / м³

Из (1) следует, что 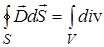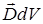. (19)

Из сравнения (18) и (19) находим,что 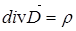. (20)

Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет

следующий вид: 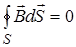, (21) 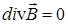. (22)

12.4. Полная система уравнений Максвелла в дифференциальной форме

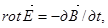
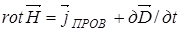. (23)

, .

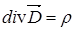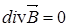Эту систему уравнений необходимо дополнить материальными уравнениями, характе­ризующими электрические и магнитные свойства среды:

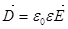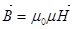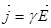, , . (24)

Итак, после открытия взаимосвязи между электрическими и магнитным полями ста­ло ясно, что эти поля не существуют обособлено, независимо одно от другого. Нельзя соз­дать переменное магнитное поле без того, чтобы одновременно в пространстве не возникло и электрическое поле.

Отметим, что покоящийся в некоторой системе отсчета электрический заряд создает только электростатическое поле в этой системе отсчета, но он будет создавать магнитное поле в системах отсчета, относительно которых он движется. То же самое относится и к неподвижно­му магниту. Заметим также, что уравнения Максвелла инвариантны к преобразованиям Лоренца: причем для инерциальных систем отсчета К и К’выполняются следующие соотношения: 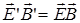, 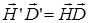. (25)

На основании изложенного можно сделать вывод, что электрические и магнитные поля являются проявлением единого поля, которое называют электромагнитным полем. Оно распространяется в виде электромагнитных волн.

При написании конспекта лекций использовались известные учебники по физике, изданные в период с 1923 г. (Хвольсон О.Д. «Курс физики») до наших дней (ДетлафА.А., Яворский Б.М., Савельев И.В., Сивухин Д.В., Трофимова Т.И., Суханов А.Д., и др.)

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ФИЗИКЕ

ЧАСТЬ II

1. Электрический заряд. Дискретность заряда. Закон сохранения заряда. Закон Кулона (1.1, 1.2)*.

2. Электрическое поле. Напряженность электрического поля точечного заряда (1.3).

3. Принцип суперпозиции электрических полей. Силовые линии (1.4).

4. Электрический диполь. Поле электрического диполя (1.5).

5. Момент силы, действующий на диполь в электрическом поле. Энергия диполя в электрическом поле (1.5).

6. Поток вектора напряженности. Теорема Гаусса-Остроградского для электростатического поля в вакууме (2.1, 2.2).

7. Поле равномерно заряженной, бесконечно протяженной полскости. Поле между двумя бесконечно протяженными разноименно заряженными параллельными плоскостями (2.2.1, 2.2.2).

8. Поле заряженного цилиндра. Поле заряженной сферы (2.2.3, 2.2.4).

9. Работа сил электростатического поля. Циркуляция вектора напряженности электрического поля (3.1).

10. Потенциальный характер электростатического поля. Потенциал (заключение 3.1, 3.2).

11. Потенциал поля точечного заряда и поля, создаваемого системой точечных зарядов. Разность потенциалов (3.2).

12. Эквипотенциальные поверхности (3.3).

13. Связь между напряженностью электрического поля и потенциалом (3.4).

14. Электрическое поле в диэлектриках. Полярные и неполярные диэлектрики. Дипольный момент диэлектрика (4, 4.1).

15. Поляризация диэлектриков: ориентационная и ионная. Вектор поляризованности (4.2).

16. Напряженность электрического поля в диэлектрике. Диэлектрическая проницаемость (4.3).

17. Теорема Гаусса – Остроградского для поля в диэлектрике. Связь векторов 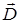– смещения, 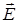– напряженности и 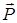– поляризованности (4.4).

18. Проводники в электростатическом поле (5.5.1).

19. Электрическая емкость уединенного проводника. Электрическая емкость конденсатора. Плоский конденсатор (5.2).

20. Энергия заряженного проводника, системы заряженных проводников и конденсатора (5.3).

21. Энергия электрического поля. Объемная плотность энергии электрического поля в диэлектрике и вакууме (5.4).

22. Электрический ток. Характеристики электрического тока: сила тока, вектор плотности тока (6.1).

23. Электродвижущая сила источника тока. Напряжение (6.2).

24. Закон Ома для однородного участка цепи. Электрическое сопротивление, удельное сопротивление. Зависимость сопротивления проводников от температуры (6.3.1).

25. Закон Ома в дифференциальной форме. Удельная электропроводность (6.3.2).

26. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи (6.4).

27. Закон Джоуля – Ленца. Работа и мощность тока. КПД источника (6.5).

28. Закон Джоуля – Ленца в дифференциальной форме (6.6).

29. Магнитное поле в вакууме. Магнитный момент контура с током. Вектор магнитной индукции. Силовые линии магнитного поля (8.1).

30. Закон Био-Савара-Лапласа. Принцип суперпозиции магнитных полей (8.3).

31. Магнитное поле прямого тока (8.3.1).

32. Магнитное поле кругового тока (8.3.2).

33. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля (9.1).

34. Магнитное поле соленоида (9.1.1).

35. Магнитный поток. Теорема Гаусса для магнитного поля (9.2).

36. Работа перемещения проводника с током в постоянном магнитном поле (9.3).

37. Действие магнитного поля на движущийся заряд. Силы Лоренца (8.2, 9.4).

38. Магнитное поле в веществе. Магнитные моменты атомов. Вектор намагниченности. Напряженность магнитного поля. Магнитная проницаемость вещества (10.1, 10.2).

39. Теорема о циркуляции вектора напряженности магнитного поля (10.3).

40. Виды магнетиков: диамагнетики, парамагнетики, ферромагнетики. Магнитная проницаемость и магнитное поле магнетиков (10.4).

41. Закон электромагнитной индукции. Закон Ленца (11.1).

42. Явление самоиндукции. Индуктивность. Электродвижущая сила самоиндукции (11.2).

43. Токи при размыкании и замыкании цепи (11.3).

44. Энергия магнитного поля. Объемная плотность энергии магнитного поля (11.4).

45. Первое уравнение Максвелла (12.1).

46. Ток смещения. Второе уравнение Максвелла (12.2).

47. Третье и четвертое уравнение Максвелла (12.3).

48. Полная система уравнений Максвелла в дифференциальной форме. Материальные уравнения (12.4).

* В обозначении (1.1., 1.2) первая цифра означает номер лекции, а вторая – номер параграфа в этой лекции, где изложен материал по данному вопросу.

Дата добавления: 2014-03-11; просмотров: 784; Нарушение авторских прав

Мы поможем в написании ваших работ!