Аксиомы теории вероятностей

Предложенное выше определение вероятности наряду с очевидными достоинствами, прежде всего простотой и интуитивной наглядностью, имеет и ряд существенных недостатков: предусматривает только конечное или счётное множество элементарных событий и обязательно знания их вероятностей. Всё это далеко не всегда имеет место, и поэтому введённое определение не является достаточно общим. В настоящее время стало общепринятым аксиоматическое построение теории вероятностей.

Сформулируем теперь аксиомы теории вероятностей. Пусть W - пространство элементарных событий некоторого стохастического эксперимента, и в W выделена система F событий, являющаяся алгеброй событий. Это означает, что:

WÎF;

если A Î F Þ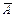Î F;

если A и B Î F Þ A + B и AB Î F.

Предположим, что каждому событию A Î F поставлено в соответствие число p(A) - вероятность случайного события A и верны свойства:

1: p(A) ³ 0 для любого A Î F;

2: p(W) = 1;

3: если A и B несовместны (AB = Æ), то p(A + B) = p(A) + p(B).

В таком виде аксиоматика теории вероятностей была предложена А.Н. Колмогоровым и оказалась исключительно плодотворной для её развития. Введённая таким образом тройка (W, F, p) называется вероятностным пространством. Этот подход позволяет, не обсуждая трудного вопроса о том, откуда известны первоначальные вероятности, по известным вероятностям одних событий вычислять вероятности других, достаточно сложных событий, пользуясь только перечисленными аксиомами.

Дата добавления: 2014-03-11; просмотров: 687; Нарушение авторских прав

Мы поможем в написании ваших работ!