
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Косвенный МНК (КМНК)
|
Читайте также: |
Он используется в случае идентифицируемых моделей. Его процедура включает три этапа. На первом этапе структурная модель преобразуется в приведенную форму, на втором - для каждого уравнения приведенной формы с помощью МНК оцениваются приведенные коэффициенты. На третьем этапе производится обратный переход к структурной форме, то есть оцениваются структурные коэффициенты.
Пусть имеем следующие наблюдения случайной величины:
| № наблюдения | у1 | у2 | х1 | х2 | 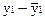 (у1)
(у1)
| 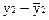 (у2)
(у2)
| 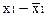 (х1)
(х1)
| 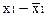 (х2)
(х2)
|
| 0,9 | 31,3 | 18,9 | -1,185 | 9,97 | 1,99 | -30,55 | ||
| 1,7 | 13,4 | 13,7 | -0,385 | -7,93 | -3,21 | -9,55 | ||
| 0,7 | 4,5 | 18,5 | -1,385 | -16,83 | 1,59 | -49,55 | ||
| 0,65 | 7,3 | 4,8 | 50,2 | -1,435 | -14,03 | -12,11 | -23,35 | |
| 2,6 | 21,8 | 0,515 | -0,33 | 4,89 | 32,45 | |||
| 1,3 | 15,6 | 5,8 | 96,6 | -0,785 | -5,73 | -11,11 | -23,05 | |
| 4,1 | 36,1 | 2,015 | 13,67 | 19,19 | 49,45 | |||
| 1,6 | 17,9 | 20,1 | 85,6 | -0,485 | -3,43 | 3,19 | 12,05 | |
| 6,9 | 4,815 | 43,67 | 11,09 | 65,45 | ||||
| 0,4 | 2,3 | 1,4 | 4,1 | -1,685 | -19,03 | -15,51 | -69,45 | |
| среднее | 2,085 | 21,33 | 16,91 | 73,55 |
Рассматриваемая структурная модель имеет вид:
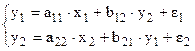
Эта модель точно идентифицируема.
Приведенная форма модели имеет вид:
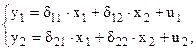
где u1 , u2 – случайные ошибки в приведенной форме модели.
Оценим коэффициенты в приведенной модели, подразумевая под у и х отклонения 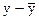 и
и 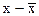 . Получим:
. Получим:
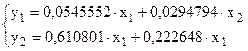
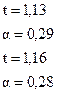
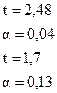
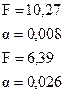
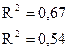
В принципе, модель вполне значима, хотя коэффициенты в силу малого числа наблюдений незначимы (кроме 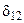 ).
).
Далее необходимо от этой приведенной формы перейти к структурной по формулам:
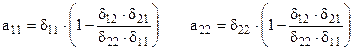 ,
, 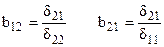 ,
,
следовательно,
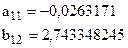
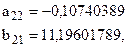
или
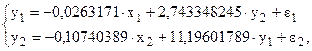
т. е. задача решена.
Если же непосредственно применить МНК к исходному структурному уравнению, то получим:
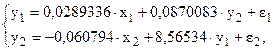
т. е. совершенно другие коэффициенты, которые являются смещенными и несостоятельными.
| <== предыдущая страница | | | следующая страница ==> |
| Взаимозависимых уравнений | | | Формы системы эконометрических уравнений |
Дата добавления: 2014-03-19; просмотров: 353; Нарушение авторских прав

Мы поможем в написании ваших работ!