Взаимозависимых уравнений

Уравнений. Проблема идентификации в системах

Параметры независимых и рекурсивных систем уравнений оцениваются с помощью МНК, а для оценки параметров взаимосвязанных уравнений нужны специальные приемы, т.к. непосредственное использование МНК в данном случае дает смещенные и несостоятельные оценки.

Для определения параметров в таких моделях в первую очередь систему взаимосвязанных уравнений преобразуют из структурной формы в приведенную форму, которая представляет собой систему линейных функций эндогенных переменных от экзогенных (т.е. преобразуют исходную систему в систему независимых уравнений):

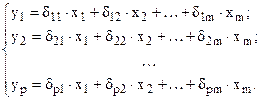
Эндогенные переменные – это взаимозависимые переменные, которые определяются внутри модели. Их число равно числу уравнений в системе.

Экзогенные переменные – это независимые внешние переменные (факторы), влияющие на эндогенные переменные.

Коэффициенты а и b, фигурирующие в структурной форме, называются структурными коэффициентами; коэффициенты δ в приведенной форме (приведенные коэффициенты) представляют собой нелинейные функции структурных коэффициентов.

Например, для структурной модели вида

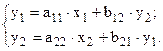
приведенная форма модели имеет вид:

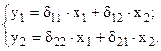
Определим значения приведенных коэффициентов δ.

y₂ из первого уравнения структурной модели можно выразить следующим образом:

.

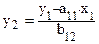Тогда система структурных уравнений примет вид:

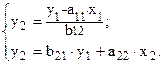
Откуда имеем равенство:

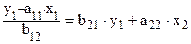или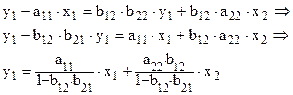

Обозначая

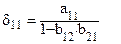и ,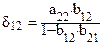

получим первое уравнение структурной модели в приведенной форме:

.

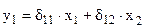Аналогично выразим переменную y₁ из второго структурного уравнения модели:

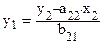
и запишем это выражение в левой части первого уравнения структурной формы модели:

,

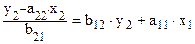откуда

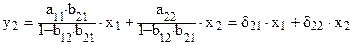
Таким образом, получим приведенную систему уравнений:

,

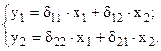где δ выражены через а и b.

При этом число приведенных коэффициентов равно числу структурных коэффициентов, и переход от структурных коэффициентов к приведенным однозначен.

В то же время, например, в структурной модели

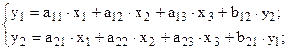
имеется 8 структурных коэффициентов, а в соответствующей ей приведенной форме

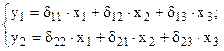
приведенных коэффициентов всего 6. И если с помощью МНК оценены эти 6 коэффициентов, то обратный переход от приведенных коэффициентов к структурным называется проблемой идентификации. В данном случае идентификация – единственность соответствия между приведенной и структурной формами модели.

С позиции проблемы идентификации структурные модели можно разделить на 3 вида:

§ Идентифицируемые, когда число структурных и приведенных коэффициентов одинаково.

§ Неидентифицируемые, когда число структурных коэффициентов больше числа приведенных коэффициентов.

§ Сверхидентифицируемые, когда число структурных коэффициентов меньше числа приведенных коэффициентов.

Таким образом, проблема оценки параметров системы взаимосвязанных эконометрических уравнений состоит в том, что оценивать непосредственно с помощью МНК параметры структурной модели нельзя, т.к. оценки будут смещенными и несостоятельными. Для того, чтобы получить качественные оценки, от структурной формы нужно перейти к приведенной и произвести с помощью МНК оценку параметров приведенной формы. Затем от полученных оценок перейти к оценкам параметров структурной формы. Но при этом возникает проблема идентификации, т.к. такой переход не всегда возможен. Он вполне возможен для идентифицируемых моделей. В этом случае применяется косвенный МНК (КМНК), который возможен и в случае сверх идентифицируемых моделей. В этом случае используется двух шаговый МНК, который также можно использовать и в случае идентифицируемых моделей.

Дата добавления: 2014-03-19; просмотров: 522; Нарушение авторских прав

Мы поможем в написании ваших работ!