Выбор уравнений регрессии

Выбираться должно уравнение, которое лучше других описывает связь Y с Х. Если преимущество более сложной функции над более простой мало, лучше ограничиться более простой. Наконец, надо брать функции, которые не противоречат здравому смыслу.

Линейное или нелинейное уравнение?

При строго линейной зависимости коэффициенты корреляционного отношения h_yx² и h_xy² равны между собой и равны r_xy², т.е. n=h²-r²=0. При нелинейной связи n¹0.

Если по F-критерию Фишера разность n значима, лучше использовать нелинейное аналитическое сглаживание (F= ).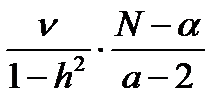

Какое нелинейное сглаживание (уравнение)?

Нередко возможные уравнения подбирают на основании сравнения эмпирического графика с известными образцами кривых.

Обычно проверяют на ПК несколько возможных функций, для которых оценивается и так называемая среднеквадратичная ошибка аппроксимации.

Предпочтение отдается той функции, которая обнаруживает явно меньшую ошибку аппроксимации.

Выбор функции - наука, но в некоторой степени и искусство.

Если коэффициент корреляции велик и высоко значим, а принята, например, периодическая функция, говорят о значимой линейной компоненте изменчивости, на которую наложена циклическая изменчивость. Возможно наложение одних функций на другие.

Пример.

Анализ временного ряда

Исследуется уже приводившийся ряд данных: урожайность озимой пшеницы в Луганской области по годам с 1945 г. по 2004 г. (за 60 лет). Данные облстата.

Здесь на рис. 6 Х – годы, Y – урожайность озимой пшеницы в ц/га.

Рис. 6. Сглаживание временного ряда прямой линией

Корреляция годы – урожайность максимально значимая (r=0.541***, r²=0.293). Линейная компонента изменчивости очевидна (рис. 6).

Уравнение линейной регрессии y=12.18+0.2748x. Угловой коэффициент 0.2748, т.е. на данном 60-и летнем временном интервале происходил рост урожайности в среднем на ~ 0.275 ц/га (на ~ 1 ц/га за 4 года).

Среднеквадратичная погрешность аппроксимации прямой линией Е=47.55.

На глаз кажется, что в последние 10-15 лет урожайность перестала расти и даже несколько снизилась (рис. 6). Это требует проверки посредством сглаживания криволинейными функциями.

Дата добавления: 2014-07-19; просмотров: 379; Нарушение авторских прав

Мы поможем в написании ваших работ!