В моделях множественной регрессии

Подходы к устранению мультиколлинеарности

Существует ряд подходов преодоления мультиколлинеарности:

1. Самый простой путь – исключение из модели одного или нескольких факторов, ответственных за мультиколлинеарность.

2. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Основным методом такого рода является метод главных компонент (компонентный анализ)

3. Путем учета внутренней корреляции факторов является также переход к совмещенным уравнениям регрессии, то есть к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Например, для 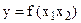возможно построение совмещенного уравнения вида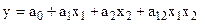. Эта зависимость включает взаимодействия первого порядка. При большом числе переменных возможно включение в модель взаимодействий более высокого порядка. Проблема: возникают трудности с интерпретацией параметров. Выбор формы уравнения регрессии производится исходя из содержательного анализа явлений и имеющегося фактического материала. Чаще всего используются линейные модели множественной регрессии.

Дата добавления: 2014-03-19; просмотров: 358; Нарушение авторских прав

Мы поможем в написании ваших работ!