Множественной регрессии

Оценка мультиколлинеарности в моделях

Для оценки мультиколлинеарности факторов используется определитель матрицы парных коэффициентов корреляции (между факторами). Например, для зависимости 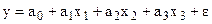. Матрица парных коэффициентов корреляции между факторами при коррелированных 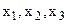имела бы определитель, равный 1, т. е.

,

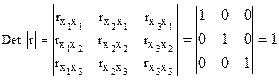так как 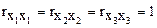, а .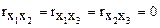

При полной линейной зависимости между факторами все коэффициенты корреляции равны 1, определитель этой матрицы равен 0, так как

.

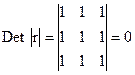Таким образом, чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов.

Оценка значимости мультиколлинеарности факторов может быть проведена путём проверки гипотезы о независимости факторов – H₀: 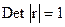. Доказано, что величина

,

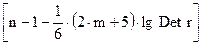где n – число наблюдений,

m – число факторов,

имеет распределение, близкое к 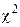с 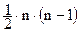степенями свободы. И если фактическое значение 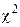больше табличного (критического) :

,

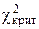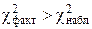то гипотеза H₀ отклоняется (т. к. ошибка первого рода слишком велика). Это значит, что 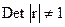, и мультиколлинеарность имеет место.

Факторы, ответственные за мультиколлинеарность можно определить коэффициенты множественной детерминации R². Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значения коэффициента множественной детерминации фактора к 1, тем выше мультиколлинеарность, вносимая данным фактором. Сравнивая между собой коэффициенты множественной детерминации факторов, можно выделить переменные, ответственные за мультиколлинеарность, и решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной множественной детерминации.

Коэффициент (индекс) детерминации:

,

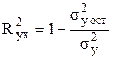где 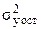– дисперсия остатков (e), 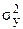– дисперсия y.

Пусть, например, матрица парных коэффициентов корреляции имеет вид:

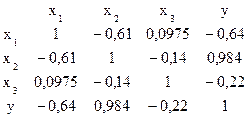
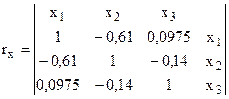
Определим, насколько велика мультиколлинеарность факторов:

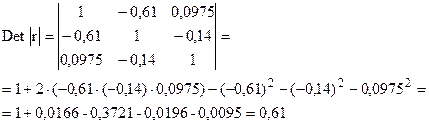
Определим значимость полученного показателя (если ,),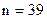

.

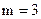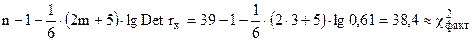
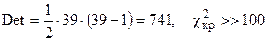Следовательно, нулевая гипотеза 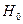: 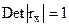не отклоняется. Однако, получаемые значения 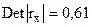недалеко от 1, поэтому определим факторы, в наибольшей степени ответственные за мультиколлинеарность:

Зависимые переменные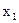
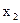
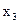
Независимые переменные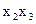
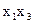
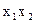
Коэффициент детерминации,	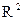0,368	0,375	0,02

Таким образом, за мультиколлинеарность в одинаковой степени ответственны 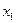и 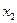. В то же время, при отборе факторов нужно учесть, что наиболее сильная связь имеет место между 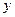и 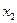, а между 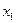и 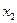связь также довольно сильна. Поэтому в первую очередь нужно отбросить 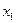. Тогда получим: 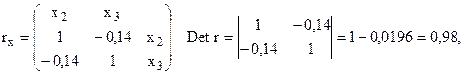т. е. очень близко к 1, т. е. мультиколлинеарность практически отсутствует.

Поэтому, в принципе, в модели целесообразно оставить два фактора: 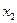и 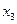, хотя можно ожидать, что модель будет достаточно хорошей и том случае, если оставить лишь .

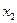Регрессионные модели в этих двух случаях будут иметь вид:

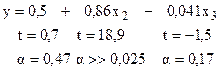
Т. е. модель в целом значима и значим коэффициент при 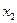, однако коэффициент при 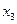и свободный член незначимы.

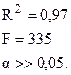
Следовательно, качество модели в целом, судя по величине критерия Фишера, во втором случае улучшилась. Следовательно, в данном случае имеет место парная регрессионная модель.

Дата добавления: 2014-03-19; просмотров: 388; Нарушение авторских прав

Мы поможем в написании ваших работ!