
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Множественной регрессии. Фиктивные переменные модели
Фиктивные переменные модели
До сих пор в качестве факторов рассматривались экономические переменные, принимающие непрерывные или дискретные значения в некотором интервале. Вместе с тем, может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть различные атрибутивные признаки (пол, профессия, образование, принадлежность к определенному региону). Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены цифровые метки - тем самым качественные переменные преобразуются в количественные. Такие сконструированные переменные в эконометрике называют фиктивными переменными (в отечественной литературе их иногда называют структурными переменными).
Рассмотрим пример.
Для нескольких предприятий получены следующие данные:
| № предприятий | ||||||||
| Рентабельность (y) | 14,5 | 9,8 | ||||||
| Уровень качества продукции (x) | 0,36 | 0,29 | 0,13 | 0,61 | 0,49 | 0,78 | 0,23 | 0,69 |
Необходимо определить зависимость рентабельности от уровня качества.
Решение.
Регрессионная зависимость имеет вид
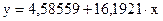 ;
;
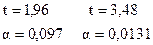
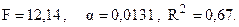
В принципе, модель существенна.
Разобьем уровень качества на 2 части: высокий и низкий уровень качества: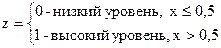
| № предприятий | ||||||||
| Рентабельность (y) | 14,5 | 9,8 | ||||||
| Уровень качества продукции (z) |
Получим уравнение регрессии
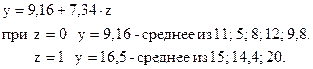
| <== предыдущая страница | | | следующая страница ==> |
| Показатель | | | Предпосылки метода наименьших квадратов |
Дата добавления: 2014-03-19; просмотров: 341; Нарушение авторских прав

Мы поможем в написании ваших работ!