
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Показатель
Анализ влияния факторов на результативный
Вопрос включения факторов в модель множественной регрессии, как уже было показано выше, является одним из ключевых. Поэтому этот вопрос рассматривается на различных этапах построения эконометрической модели. Вначале на основе качественных экономических представлений об изучаемом явлении определяются влияющие факторы, как правило, с большим избытком, затем с помощью матрицы парных коэффициентов корреляции и анализа мультиколлинеарности отбрасываются несущественные факторы. Существенность факторов в дальнейшем проверяется с помощью t-статистик после построения модели, и вновь могут быть отброшены несущественные факторы.
В данном параграфе рассматриваются методы, дополняющие анализ существенности факторов с помощью t-статистик.
1. Анализ существенности факторов с помощью коэффициентов эластичности.
Коэффициент эластичности показывает, на сколько процентов в среднем изменится величина результативного показателя y при изменении объясняющего фактора x на 1 %. Коэффициент эластичности определяется по формуле:

Для линейной функции 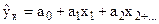
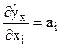
Для примера, рассмотренного в п.2.9:
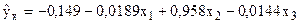
В середине интервала:
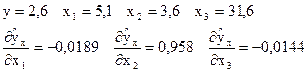
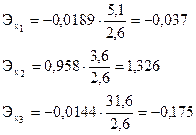
Отсюда видно высокое влияние фактора х2 и низкое влияние факторов х1 и х3.
Коэффициент эластичности в среднем определяется как
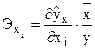 .
.
2. Определение стандартизованных коэффициентов регрессии.
Уравнение регрессии в стандартизованном масштабе имеет вид:
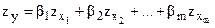 ,
,
где 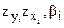 - стандартизованные переменные.
- стандартизованные переменные.
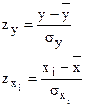
Для этих переменных 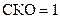 , а среднее значение равно 0.
, а среднее значение равно 0.
В силу того, что 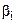 центрированные и нормированные, они сравнимы между собой, и, сравнивая их друг с другом, можно выделить факторы, наиболее сильно влияющие на результативный показатель.
центрированные и нормированные, они сравнимы между собой, и, сравнивая их друг с другом, можно выделить факторы, наиболее сильно влияющие на результативный показатель.
Для рассматриваемого примера стандартизованные переменные имеют вид:
| z1 | -0,385 | -0,629 | 1,0145 | -1,116 | -0,325 | 1,44 |
| z2 | 1,527 | 0,0985 | -1,281 | -0,246 | 0,64 | -0,739 |
| z3 | 0,613 | -0,96 | 0,228 | 1,578 | -0,946 | -0,512 |
| zy | 1,49 | 0,84 | -1,074 | -0,37 | 0,79 | -0,92 |
Уравнение:
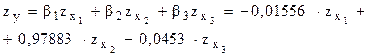
Из него видно, что наиболее существенно влияет на результат переменная 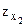 , то есть х2, влияние других переменных гораздо меньше.
, то есть х2, влияние других переменных гораздо меньше.
3. Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии. Коэффициенты частной корреляции представляют собой отношение сокращения остаточной дисперсии, имевшей место до введения его в модель.
Пример
Пусть зависимость объема продукции (у) от затрат труда (х1) характеризуется уравнением:
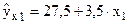 ,
,
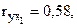
остаточная дисперсия: 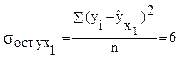 .
.
Включив в уравнение регрессии дополнительный фактор х2 – техническую оснащенность производства, получим уравнение регрессии в виде:
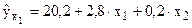
Для этого уравнения остаточная дисперсия будет меньше.
Пусть 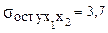 , сокращение остаточной дисперсии за счет включения дополнительного фактора составит:
, сокращение остаточной дисперсии за счет включения дополнительного фактора составит:
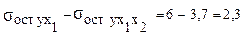 .
.
Тогда 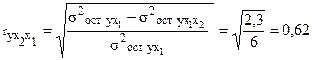
Аналогично чистое влияние на результат фактора х1:

Пусть 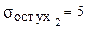 , тогда
, тогда 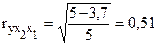 .
.
Таким образом, более сильное влияние на объем продукции оказывает техническая оснащенность.
Если выразить остаточную дисперсию через показатель детерминации 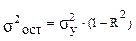 , то формула коэффициента частной корреляции примет вид:
, то формула коэффициента частной корреляции примет вид:
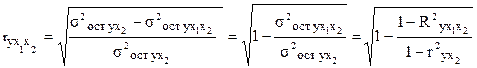
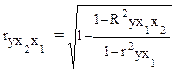 ,
,
т. е. выражается через коэффициенты парной корреляции и коэффициента множественной корреляции.
Рассмотренные показатели частной корреляции называют коэффициентами (индексами) частной корреляции первого порядка, так как они фиксируют тесноту связи двух переменных при устранении влияния одного фактора.
Аналогично рассматриваются частные коэффициенты корреляции второго и так далее порядка, то есть влияние фактора х1 можно оценить при разных условиях независимости действия других факторов.
В общем виде при наличии m факторов для уравнения 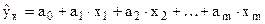 коэффициент частной корреляции, измеряющий влияние на
коэффициент частной корреляции, измеряющий влияние на 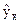 фактора хi при неизменных уровнях других факторов, можно определить по формуле:
фактора хi при неизменных уровнях других факторов, можно определить по формуле:
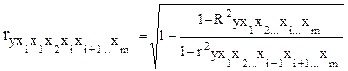 ,
,
где R – коэффициенты множественной корреляции с включенными хi и с отсутствием хi.
Таким образом, для определения частных коэффициентов корреляции необходимо иметь матрицу парных коэффициентов корреляции, по которой можно определить R2.
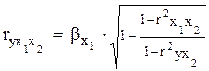
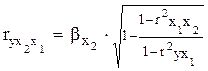 .
.
В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения, используются только на стадии формирования модели в процедуре отбора факторов.
В рассмотренном примере частные коэффициенты корреляции имеют следующие значения:
| Х1 | Х2 | Х3 | Y | |
| X1 | -0,0391 | -0,4089 | -0,0793 | |
| X2 | 0,224 | 0,9823 | ||
| X3 | -0,2732 | |||
| Y |
Отсюда также следует высокая зависимость у от х2 и низкая зависимость от остальных факторов.
| <== предыдущая страница | | | следующая страница ==> |
| Оценка погрешности регрессионной модели | | | Множественной регрессии. Фиктивные переменные модели |
Дата добавления: 2014-03-19; просмотров: 339; Нарушение авторских прав

Мы поможем в написании ваших работ!