Множественной регрессии. Непосредственная оценка параметров

Непосредственная оценка параметров

После выполнения этапа спецификации начинается выполнение этапа идентификации. Первым шагом этого этапа является оценка параметров регрессии. Для этого чаще всего используется метод наименьших квадратов, который заключается в таком подборе параметров регрессии, при значении которых квадрат случайной составляющей минимален, то есть 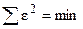, или в общем случае для уравнения 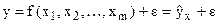получим:

.

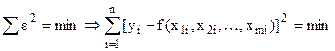В случае линейной зависимости:

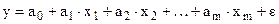
имеем .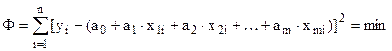

Для нахождения параметров 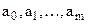необходимо взять частные производные по этим параметрам и приравнять их к 0:

.

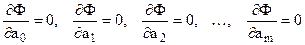При этом получается система линейных уравнений:

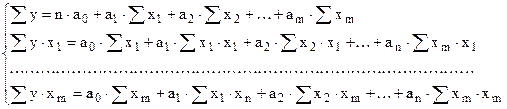
Ее решение может быть осуществлено методом определителей:

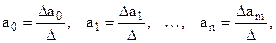
где 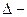определитель системы;

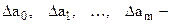частные определители.

При этом:

,

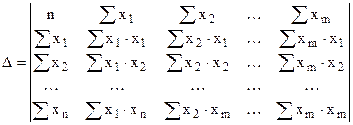а 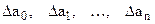получаются из 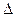путем замены соответствующего столбца матрицы определителя данными левой части системы уравнений.

Например:

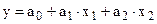
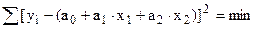
Система уравнений :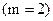

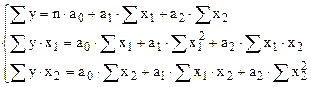
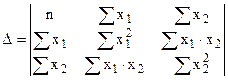
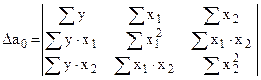
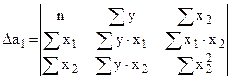
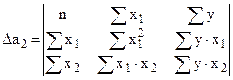
В простейшем случае парной регрессии 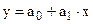получим:

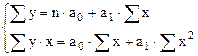
Разделим 1-ое и 2-ое уравнения на n:

,

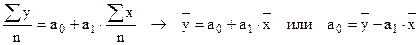подставив во 2-ое уравнение, получим:

,

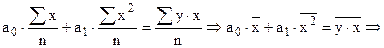
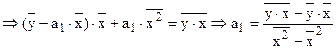или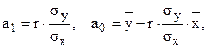

где r – коэффициент корреляции.

Это получается следующим образом:

.

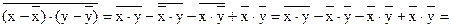
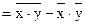С другой стороны:

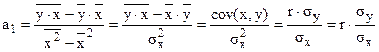
При

Дата добавления: 2014-03-19; просмотров: 328; Нарушение авторских прав

Мы поможем в написании ваших работ!