При построении модели множественной регрессии

Особенности проведения этапа спецификации

Раздел 2. Модели множественной регрессии

Виды эконометрических моделей

Эконометрические модели классифицируются следующим образом:

§ в зависимости от учета фактора времени:

- одновременные;

- динамические;

§ в зависимости от количества объясняющих переменных (признаков):

- парные;

- множественные;

§ в зависимости от формы модели:

- линейные;

- нелинейные;

§ в зависимости от числа результатных переменных (признаков):

- одно уравнение;

- системы уравнений.

В качестве переменных в эконометрических моделях могут использоваться как непрерывные, так и дискретные, но обязательно количественные. Следовательно, качественные признаки должны быть преобразованы в количественные путем введения оценочных шкал или фиктивных переменных.

Общее уравнение множественной регрессии имеет вид:

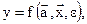
где 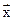- вектор переменной,

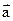- вектор параметра.

В простейшем случае эта модель является линейной:

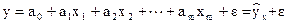
В случае если наиболее существенным является один фактор, то эта модель преобразуется в модель парной линейной регрессии:

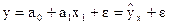
Таким образом множественная регрессия имеет место в случае, когда на результатную переменную существенно влияют несколько факторов и при этом они не зависят друг от друга.

Построение модели регрессии начинается с этапа спецификации модели, т.е. с определения результатной переменной, выявления и отбора влияющих факторов, получения данных, характеризующих переменные, выявления формы зависимости (линейной или нелинейной).

Включение факторов в регрессионную модель связано прежде всего с природой взаимосвязи результатной переменной с явлениями, характеризующимися включаемыми факторами. Поэтому основными требованиями, предъявляемыми к факторным переменным, наряду с их количественной измеримостью, является их сильная взаимосвязь с результатной переменной и слабая связь между собой. При высокой интеркорреляции система нормальных уравнений, которая строится для определения оценок параметров модели, может оказаться плохо обусловленной и повлечь за собой ненадежность этих оценок, параметры регрессионного уравнения оказываются неинтерпретируемыми.

Включаемые в модель множественной регрессии факторы должны объяснять вариацию зависимой переменной. При включение в модель следующего фактора объясняемость зависимой переменной должна возрастать, а вариация остатков – уменьшаться. Если это не так, то включаемый фактор не улучшает модель, является лишним или вредным. Насыщение модели лишними факторами может привести к статической незначимости параметров регрессии.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости.

Однако предварительный факторный теоретический анализ часто не позволяет однозначно ответить на вопрос о целесообразности включения тех или иных факторов в модель. Поэтому отбор факторов осуществляется в два этапа:

§ на первом подбираются факторы, исходя из сущности проблемы;

§ на втором – на основе анализа матрицы коэффициентов парной корреляции и на основе других статистических методов.

Коэффициентыинтеркорреляции, выявляемые с помощью матрицы парных коэффициентов корреляции, позволяют исключать из модели дублирующие факторы.

Пусть, например, при изучении зависимости 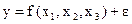матрица парных коэффициентов корреляции имеет вид:

	y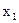
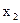
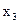
y		0,8	0,7	0,85
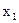
	0,8		0,8	0,7
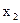
	0,7	0,8		0,1
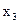
	0,85	0,7	0,2

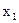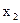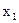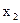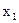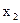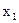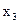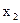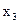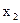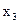Здесь высокая корреляция между и , то есть они дублируют друг друга. При этом возникает вопрос, какой из факторов, или включать в модель. На первый взгляд между y и коэффициенты корреляции выше, чем между y и , однако между и гораздо выше коэффициент корреляции, чем между и . Поэтому в модель целесообразно ввести и . Таким образом получается зависимость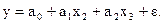

По величине парных коэффициентов корреляции обнаруживается только явная интеркорреляция факторов. Однако, наибольшие трудности при построении модели множественной регрессии возникают при мультиколлинеарности факторов, когда более чем два фактора связаны между собой существенной зависимостью, и имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности означает, что несколько факторов всегда будут действовать одинаково, и в результате вариация в исходных данных не будет независимой. Поэтому нельзя будет оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК.

Дата добавления: 2014-03-19; просмотров: 433; Нарушение авторских прав

Мы поможем в написании ваших работ!