Алгоритмы и математические модели тестирования

Довольно распространенным методом контроля уровня знаний обучаемого контингента, в настоящее время является тестирование, которое также представляет определенную диалоговую форму обучения и обычно реализуется в рамках соответствующей информационной технологии. Особенно популярным в последнее время становится компьютерное адаптивное тестирование (Computerized Adaptive Testing – CAT), при котором компьютер отбирает задания в зависимости от предыдущих ответов, подстраивая тест к уровню тестируемого. Основой для современных компьютерных адаптивных тестов служит теория ответа на задание (Item Response Theory – IRT), учитывающая уровень тестируемого и трудность задания [9].

Процедура тестирования описывается киберсистемой из двух конечных автоматов А и А', соединенных по схеме рис.4.1, и алгоритм их поведения представляет частный случай общего алгоритма диалога, приведенного в табл. 4.1, в том смысле, что алгоритм тестирования реализуется в одном цикле. Формально тест представляет собой слово z = z₁z₂…z_n в алфавите Z, так, что каждая буква z_i 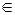Z, 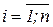- это i-ое задание теста z. Данный тест z поступает на вход автомата А' (тестируемый объект) и обрабатывается как слово в соответствии с алгоритмом (1.1);(1.3), который в данном случае задает процедуру «решения» тестовых заданий. 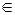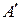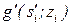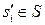На основе данных решений по каждому заданию z_i дается ответ a_i= , где – вариант решения, предложенный тестируемым по заданию z_i. В результате, посредством алгоритма (1.2), на выходе А' формируется слово a = a₁a₂…a_n; a_i 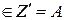, которое для контроля поступает на вход A автомата А. Контроль ответа сводится к тому, что каждая буква a_i слова a сравнивается с результатом правильного решения 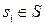и ответ a_i приобретает рейтинг 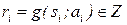. В итоге на выходе А формируется слово r = r₁r₂…r_n, по которому устанавливается общий результат выполнения теста z, этот результат доводится до А' и на этом процедура тестирования завершается.

В российском образовательном пространстве в процедурах компьютерного тестирования в основном преобладают тесты с открытой или закрытой формой заданий [9;10]. При закрытой форме тестовых заданий (формат multiple choice) каждое такое задание снабжено набором ответов, из которых обычно только один верный, и тестируемому предлагается выбрать по одному ответу из каждого такого набора. В заданиях открытой формы ответы с выбором не предусматриваются и испытуемый должен сам представить ответ, который свидетельствует о наличии или отсутствии у него требуемых знаний по заданному вопросу. При компоновке тестовых батарей задание с закрытой формой обычно располагают в начале (часть А), а более сложные задания обычно предполагают открытую форму ответа и размещаются ближе к концу теста (часть Б).

Алгоритм обработки выполненных тестов может быть следующим [11]. Пусть, как и выше, тест z представляется словом z = z₁z₂…z_n, у которого первые k букв z_i, - описывают задания с закрытой формой, а остальные буквы z_i, 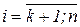- это задания с открытой формой ответов. Тогда выходное множество 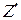автомата А' (и, соответственно, входное множество A автомата А) можно представить в виде разбиения 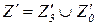(соответственно, A= 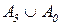), где индексы 3;0 – приписываются заданиям с закрытой и открытой формой ответов, соответственно.

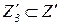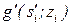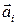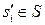Пусть при выполнении тестовых заданий с закрытой формой испытуемому по каждому отдельному заданию следует выбрать один ответ из l >1 предложенных ответов. Тогда подмножество автомата А' можно определить базисным набором l-мерных ортонормированных векторов. В этом случае = , где - вариант решения, предложенный тестируемым по заданию z_i, 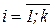, на основании которого выбран ответ 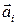(a_i1;…;a_il) 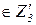, так, что одна из координат a_ij, j= 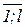, отвечающая выбранному ответу в предложенном наборе, равна 1, а остальные координаты нулевые. Из векторов 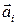сформируем столбец ( 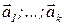)*, где * - означает операцию транспонирования, после чего, разворачивая этот столбец по координатам векторов 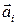, получаем матрицу ответов A_kl.

Матрица A_kl представляет входной сигнал для автомата А, который реализует контроль теста. Для этого введем вектор 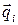(q_i1;…;q_il) 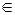A₃= 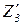, представляющий вектор-ключ к заданию z_i, 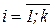, у которого одна из координат q_ij, j= 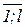, соответствующая правильному ответу в предложенном наборе, равна 1, а остальные координаты – нулевые. Из векторов 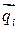сформируем строку ( ) и, затем, разворачивая координаты 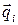в столбцы, строим ключ-матрицу Q_lk.

Легко убедиться, что для матрицы C_kk=A_klQ_lk диагональные элементы c_ii 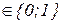, причем, c_ii=0, если дан неверный ответ к заданию z_i и c_ii=1 – в противном случае. Поэтому сумма диагональных элементов Sp(C_kk) – это количество правильных ответов среди заданий открытой формы z_i, 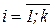теста z. Тогда, если R_kk=diag(r₁;…;r_k) – скалярная матрица рейтингов заданий z₁;…;z_k , то Sp(C_kkR_kk) – определяет общий рейтинг, оценивающий результаты выполнения теста z в части заданий с закрытой формой ответа.

При открытой форме тестовых заданий z_i, 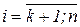, ответ к каждому заданию представляется в виде некоторого числа, так, что для подмножества 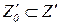можно положить 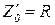. В этом случае a_i= 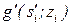, где a_i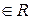 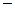численный ответ к заданию z_i в открытой форме, и можно определить вектор 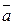(a_k+1;…;a_n). Пусть теперь 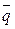(q_k+1;…;q_n) – вектор-ключ для тестовых заданий z_i, 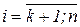, так, что q_i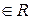 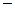правильный ответ для задания z_i. Составим разность 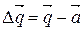, причем, координаты вектора 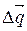запишем по правилу: 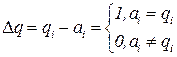(4.8)

Тогда, если 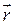(r_k+1;…;r_n) 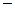есть рейтинг-вектор, где r_i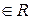 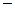рейтинг задания z_i, то скалярное произведение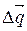 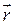определяет общий рейтинг выполнения тестовых заданий z_i с открытой формой ответа.

Общий рейтинг при выполнении теста z = z₁z₂…z_n можно определить суммой Sp(C_kkR_kk)+ 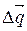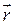, с которой связывается определенная оценочная шкала P, устанавливающая результаты тестирования, доводимые до испытуемого.

В рамках приведенного алгоритма, в Лаборатории тестирования механико-математического факультета Саратовского государственного университета им. Н.Г. Чернышевского в период 1998-2000 гг. были разработаны различные версии программных оболочек, реализующих процедуру компьютерного тестирования в режиме реального времени, а также в клиент-серверном варианте, как для работы в локальной, так и глобальной сети (с выходом в Интернет), о чем докладывалось на Всероссийских конференциях «Развитие системы тестирования в России» [12;13]. Данные компьютерные технологии с успехом апробированы в рамках школьного тестирования по математике учащихся общеобразовательных учреждений г.Саратова, для чего специально создавались довольно мощные тестовые батареи [14;15], причем, к этой работе широко привлекались студенты Саратовского госуниверситета.

В более широком формате эти технологии использовались в 2002 г. при проведении тестового мониторинга уровня подготовки выпускников I-ой ступени обучения (начальная школа) общеобразовательных учреждений Саратовской области по предметам федерального компонента – математике и русскому языку, который осуществлялся по заказу регионального Минобразования. В рамках мониторинга было охвачено 2262 школьника из всех регионов Саратовской области, заканчивающих 2001/2002 уч.г. обучение по 3-х и 4-х летним программам (для сравнения, в централизованном тестировании выпускников начальной школы 2002 г. участвовало 1074 человека). Результаты мониторинга оказались следующими: количество школьников, выполнивших тесты с оценками «4» и «5» по математике составило 77%, по русскому языку – 82% (по результатам централизованного тестирования, соответственно, 85,3% и 78,4%) [16].

Подводя некоторый итог, необходимо заметить, что, хотя информатизация современного образовательного пространства объективна и происходит довольно стремительно, все-таки процессы обучения в рамках электронной педагогики обладают тем общим недостатком, свойственным для коммуникативного общения – в этом случае субъекты общения в принципе не имеют полной логической конгруэнтности. По этой причине возникает, например, известная проблема содержательной и адекватной интерпретации результатов тестирования [10]. Поэтому можно предполагать, что класс образовательных задач, разрешимых посредством тестирования, является ограниченным, что, вообще говоря, и не оспаривается специалистами в области электронной педагогики [17].

Дата добавления: 2014-10-28; просмотров: 708; Нарушение авторских прав

Мы поможем в написании ваших работ!