Анализ и синтез в моделировании

В основе общей методологии – сочетание методов анализа и синтеза. Синтез заключается в создании описания объекта, анализ – в определении свойств объекта по его описанию, т.е. при синтезе формируются, а при анализе оцениваются проекты объектов.

Единство анализа и синтеза относится ко всем отраслям знаний, в т.ч. к моделированию. Алгоритмов «анализа – синтеза» как известно, нет – определена только общая методология (как выполняются операции анализа и синтеза).

Анализ

Взаимодействие элементов системы характеризуется прямыми и обратными связями. Сущность анализа системы состоит в том, чтобы выявить эти связи и установить их влияние на поведение всей системы в целом.

Анализ (от гр. analysis - разложение, расчленение) предполагает изучение поведения и свойств системы заданной структуры при взаимодействии с внешней средой (объект существует, необходимо исследовать его свойства - системный анализ, спектральный анализ, анализ крови и т.п.).

Разделение изучаемого объекта на части позволяет исследовать полученные части по отдельности[2]. Нелинейность характеристик объекта означает, в первую очередь, невозможность подобного разделения. Действительно, для линейных систем справедлив принцип суперпозиции, т.е. если

R = kV,

где V — воздействие, R — реакция, k — коэффициент пропорциональности, и

R₁ = kV₁ R₂ = kV₂,

то для суммарного воздействия V₃ = V₁ + V₂ будет справедливо

R₃ = k(V₁ + V₂) = kV₁ + kV₂ = R₁ + R₂,

т.е. суммарная реакция R₃ будет равна сумме реакций на отдельные воздействия.

Если же реакция на воздействие нелинейна, например, R = kV²,

то принцип суперпозиции перестает выполняться и

R₃ = k(V₁ + V₂)² ≠ kV₁ + kV₂

Таким образом, мы уже не можем заменить изучение реакции системы на сложное воздействие R₃ изучением ее реакций на более простые воздействия R₁ и R₂.

Цель исследований при анализе – качественная и количественная оценка свойств системы, различных стратегий управления процессами, характеристик элементов и их совокупностей. Основной процедурой анализа является построение обобщенной модели, адекватно отображающей интересующие исследователя свойства реальной системы и ее взаимосвязи. Характеристики процессов определяются как функции параметров системы.

Чтобы разобраться в системе, изучить, исследовать её (задача анализа), надо описать систему, зафиксировать ее свойства, поведение, структуру и параметры, то есть построить одну или несколько моделей.

Для этого надо ответить на три основные вопроса:

- что делает система (узнать поведение, функцию системы);

- как устроена система (выяснить структуру системы);

- каково качество системы (насколько хорошо она выполняет свои функции).

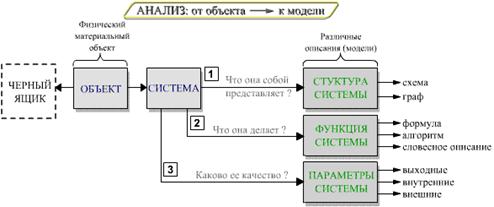
Описание объекта как системы

Между различными видами параметров, существует некоторая зависимость: выходные параметры объекта (а, значит, и его качество), зависят от входных воздействий, параметров внешней среды и от качества составляющих объект элементов (Х-параметров).

Такая зависимость представляется в аналитической форме и называется глобальной (интегративной) функцией объекта.

Существование глобальной функции ещё не означает, что она известна исследователю или проектировщику объекта - необходимо отыскать эту функцию.

Если глобальную функцию не удается представить в аналитической форме, для сложных объектов приводится алгоритмическое описание объекта (в виде поведенческой имитационной модели).

Примеры методов анализа - часто применяемые в математике аналитические методы: разложение функций в ряды, спектральный анализ, дифференциальное и интегральной исчисление и др.; в физике – методы молекулярной динамики; на производстве – конвейерная технология изготовления.

Дата добавления: 2014-08-04; просмотров: 789; Нарушение авторских прав

Мы поможем в написании ваших работ!