Алгоритм синтеза многосвязных автономно-инваринатных ЦСУ

Применение схем связанного управления при наличии внешних возмущений, не обеспечивает оптимального режима работы технологического объекта. В этом случае получить наилучшее качество управления объектом позволяет синтез и использование связно-комбинированных цифровых систем управления (СКЦСУ), существенно снижающих, а иногда и полностью исключающих влияние на выходную величину не только перекрестных каналов, но и внешних возмущений за
счет введения соответствующих компенсаторов (рис. 4.8).

Разработка наиболее эффективных систем этого класса связана с реализацией принципов инвариантности и автономности. Однако наличие при этом трудоемких аналитических преобразований, выполняемых при синтезе компенсаторов перекрестных связей и возмущений, затрудняют автоматизацию данных процедур и приводят к значительному усложнению, а иногда и невозможности реализации СКЦСУ.

Таким образом, необходима разработка алгоритмов и ППО, позволяющих реализовать автоматический синтез компенсаторов возмущений и перекрестных связей на средствах ЦВТ.

Поскольку подключение компенсаторов возмущений (способ соединения элементов СКЦСУ) может быть различным, что в свою очередь может оказывать существенное влияние на структуры разрабатываемых компенсаторов, то с учетом этого необходимо рассмотреть несколько вариантов СКЦСУ (рис. 4.8).

Первый способ соединения элементов СКЦСУ заключается в том, что выходы компенсаторов возмущений подаются на входы объекта (сплошная линия). Поведение СКЦСУ в данном случае описывается системой векторно-матричных уравнений:

е=y^з-y,

u^u=W_р^u·е,

u=W_к^u·u^u+W_к^f·f, (4.98)

y=W_о^u·u+W_о^f·f,

где f =[f ^[1](z),…, f ^[w](z)]^Т – вектор возмущений; W_о^f, W_к^f – матрица дискретных передаточных функций ОУ по каналам возмущений и матрица дискретных передаточных функций компенсаторов возмущений, r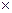w;

W_к^f=;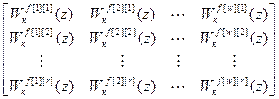

W_о^f=;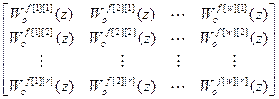

W_к^f[h][k](z)===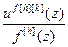

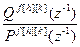
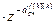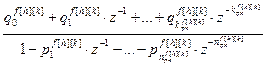
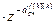=– дискретная передаточная функция компенсатора возмущения; u ^{f [h][k]}(z) – выход компенсатора возмущения; 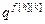, , 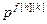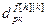– параметры дискретной передаточной функции компенсатора возмущений; , 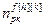– порядки числителя и знаменателя дискретных передаточных функций компенсаторов возмущений; h=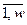, k=.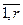

Выполнив преобразования системы (4.98) получим уравнение связи, определяющее функциональную зависимость выходов системы y от входов y^з и возмущений f:

y=(I+W_о^u·W_к^u·W_р^u)^-1·W_о^u·W_к^u·W_р^u·y^з+(I+W_о^u·W_к^u·W_р^u)^-1·(W_о^u·W_к^f+

+W_o^f)·f. (4.99)

Условие автономности остается прежним, как и в случае связной r-мерной ЦСУ без возмущений (4.30). Поэтому передаточные функции компенсаторов перекрестных связей могут быть найдены по формулам (4.34) и (4.36).

Условие инвариантности принимает вид:

W_о^u·W_к^f+W_o^f=0. (4.100)

Откуда получим выражение для расчета передаточных функций компенсаторов возмущений, удовлетворяющих условию абсолютной инвариантности:

W_к^f=(W_о^u)^-1·(-W_o^f). (4.101)

Формула (4.101) носит общий характер как при выполнении, так и при невыполнении условия автономности и сложна для расчета W_к^f вследствие необходимости вычисления обратной матрицы W_о^u при размерности объекта r>2. Однако при выполнении условия автономности, учитывая, что из (4.30):

(W_о^u)^-1=W_к^u·W_р^u·R^-1, (4.102)

можно записать эквивалентную формулу расчета передаточных функций компенсаторов возмущений:

W_к^f=W_к^u·W_р^u·R^-1·(-W_o^f). (4.103)

Выражения (4.101), (4.103) позволяют рассчитывать передаточные функции компенсаторов возмущений из условия инвариантности для первого способа подключения элементов СКЦСУ r-мерным объектом, подверженного действию w возмущающих воздействий.

Поскольку при выполнении условия автономности R является диагональной матрицей, то из (4.103) получим формулу расчета передаточной функции любого инвариантного компенсатора возмущений:

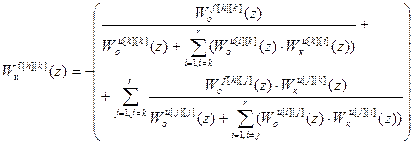(4.104)

Согласно второму способу соединения элементов СКЦСУ сигналы с выходов компенсаторов возмущений подаются на входы компенсаторов перекрестных связей (рис. 4.8, пунктирная линия).

Система уравнений, описывающая поведение СКЦСУ, примет вид:

е=y^з-y,

u^u=W_р^u·е, (4.105)

u=W_к^u·(u^u+W_к^f·f ),

y=W_о^u·u+W_o^f·f.

Выполнив подстановку получим векторно-матричное уравнение связи y с y^з и f :

y=(I+W_о^u·W_к^u·W_р^u)^-1·W_о^u·W_к^u·W_р^u·y^з+(I+W_о^u·W_к^u·W_р^u)^-1·(W_о^u·W_к^u·

·W_к^f+W_o^f)·f. (4.106)

Условие автономности остается прежним (4.30). В связи с этим передаточные функции компенсаторов перекрестных связей могут быть найдены по тем же формулам (4.34) и (4.36).

Условие инвариантности в данном случае принимает отличный от (4.100) вид:

W_о^u·W_к^u·W_к^f+W_o^f=0. (4.107)

Отсюда: W_к^f=(W_к^u)^-1·(W_о^u)^-1·(-W_o^f). (4.108)

Используя (4.102) можно получить эквивалентную формулу расчета:

W_к^f=(W_к^u)^-1·W_к^u·W_р^u·R^-1·(-W_o^f),

W_к^f=W_р^u·R^-1·(-W_o^f). (4.109)

Зависимости (4.108), (4.109) позволяют рассчитывать передаточные функции компенсаторов возмущений из условия инвариантности для второго способа соединения элементов СКЦСУ.

Обратив матрицу R и перемножив матрицы в (4.109) получим формулу расчета передаточных функций инвариантных компенсаторов возмущений:

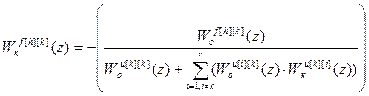. (4.110)

Третий вариант соединения элементов СКЦСУ заключается в том, что сигналы с выходов компенсаторов возмущений подаются на входы основных регуляторов вместе с ошибкой управления (рис. 4.8, штрих-пунктирная линия).

В данном случае СКЦСУ описывается следующей системой уравнений:

е=y^з-y+W_к^f·f,

u^u=W_р^u·е,

u=W_к^u·u^u, (4.111)

y=W_о^u·u+W_o^f·f.

Выполнив преобразования над (4.111) получим векторно-матричное уравнение:

y=(I+W_о^u·W_к^u·W_р^u)^-1·W_о^u·W_к^u·W_р^u·y^з+(I+W_о^u·W_к^u·W_р^u)^-1·(W_о^u·W_к^u·

·W_р^u·W_к^f+W_o^f)·f, (4.112)

которое позволяет указать условия автономности и инвариантности. Условие автономности по-прежнему остается без изменений (4.30).

Условие инвариантности в данном случае примет вид:

W_о^u·W_к^u·W_р^u·W_к^f+W_o^f=0. (4.113)

Откуда передаточные функции компенсаторов, удовлетворяющие условию абсолютной инвариантности, определяются зависимостью:

W_к^f=(W_р^u)^-1·(W_к^u)^-1·(W_о^u)^-1·(-W_o^f). (4.114)

Используя замену (W_о^u)^-1=W_к^u·W_р^u·R^-1, получим:

W_к^f=(W_р^u)^-1·(W_к^u)^-1·W_к^u·W_р^u·R^-1·(-W_o^f),

W_к^f=R^-1·(-W_o^f). (4.115)

Зависимости (4.114), (4.115) позволяют рассчитывать передаточные функции компенсаторов возмущений из условия инвариантности для третьего варианта соединения элементов СКЦСУ объектом с произвольным числом r взаимосвязанных технологических параметров подверженных действию w возмущающих воздействий.

Выполнив необходимые операции над R и W_o^f в (4.115), получим еще одну, универсальную, формулу расчета передаточных функций инвариантных компенсаторов возмущений:

.(4.116)

Анализируя полученные результаты, можно сделать следующие выводы:

1. Применение различных схем соединения элементов автономно-инвариантной ЦСУ (АвИнЦСУ) приводит к необходимости расчета передаточных функций компенсаторов возмущений по различным зависимостям. Что касается условия автономности, используемого для расчета дискретных передаточных функций компенсаторов перекрестных связей, то оно аналогично условию для r-мерной АвЦСУ без возмущений и справедливо для всех способов соединения элементов СКЦСУ;

2. Соединения элементов СКЦСУ по второму варианту позволяет получить компенсаторы возмущений с наиболее простой структурой, что снижает время, используемое на их перенастройку, и требования к характеристикам ЦВТ, используемым для ее расчета и реализации полученного алгоритма компенсации;

3. Использование принципов автономности и инвариантности при синтезе СКЦСУ позволяет представить ее в виде совокупности r одномерных (одноконтурных) систем аналогично АвЦСУ без возмущений (рис. 4.2). Это дает возможность использовать для настройки регуляторов любой из трех предложенных алгоритмов, руководствуясь при этом выводами и рекомендациями, данными в разделах 4.2.1 – 4.2.3, которые в этом случае также будут справедливы;

4. При выполнении условия автономности и невыполнении условия инвариантности СКЦСУ может быть представлена в виде совокупности r одномерных комбинированных систем (рис. 4.9), где передаточные функции 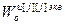(j=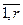) рассчитываются по зависимости (4.62). Выходы компенсаторов, показанные сплошной линией, относятся ко II варианту, а пунктирной – к III варианту. В этом случае возможно два варианта: первый – настройки компенсаторов возмущений определены заранее, второй – одновременная оптимизация настроек регуляторов и компенсаторов. И в том и в другом случае может быть использован любой из алгоритмов, описанных в разделах 4.2.2 – 4.2.3. При использовании одного и того же алгоритма оптимизации первый вариант дает незначительное увеличение размерности задачи, что приводит к небольшому росту времени, затрачиваемого на оптимизацию, и требований к характеристикам ЦВТ. Второй вариант при тех же условиях дает более существенное увеличение размерности задачи и соответственно времени оптимизации и требований к характеристикам ЦВТ;

5. Выполнение условия инвариантности и невыполнение условия автономности или отсутствие вообще компенсаторов перекрестных связей при синтезе СКЦСУ приводит к задаче оптимизации управляющей части неавтономной или несвязанной многомерной ЦСУ, подробно рассмотренной в разделе 4.2.3, размерность которой значительно больше, чем в предыдущем случае;

6. При невыполнении обеих условий получаем задачу оптимизации СКЦСУ большей, чем в предыдущем случае, размерности при заданных настройках всех компенсаторов, еще большей при заданных настройках только компенсаторов возмущений или компенсаторов перекрестных связей и максимальной размерности при одновременной настройке всей управляющей части;

7. Из выше изложенного следует, что использование принципов автономности и инвариантности позволяет не только максимально улучшить динамические свойства СКЦСУ, но и значительно увеличить быстродействие соответствующей адаптивной СКЦСУ (максимально при втором варианте подключения элементов), что позволяет вовремя проводить перенастройку управляющей части и снизить требования к используемым средствам ЦВТ. Благодаря этому возможно значительное улучшение качества управления многомерным объектом в условиях априорной и текущей неопределенности при наличии внешних возмущающих воздействий;

8. Укрупненный алгоритм синтеза (адаптации) управляющих и компенсирующих алгоритмов СКЦСУ представлен на рис. 4.10. В случае, если принцип автономности или инвариантности или и тот и другой не используются при синтезе СКЦСУ, то соответственно этапы первый и второй, второй и третий или все три могут выполняться одновременно. Отсутствие каких-либо алгоритмов управления или компенсации приводит к не выполнению соответствующего этапа.

Рис. 4.9. Укрупненный алгоритм синтеза (адаптации) многомерной ЦСУ.

Рис. 4.10. Эквивалентная структурная схема неинвариантной АвЦСУ r-мерным объектом при наличии w возмущений (II и III варианты).

Таким образом, полученные результаты позволяют осуществить выбор и синтез оптимальной с точек зрения точности, быстродействия и стоимостных затрат адаптивной многомерной ЦСУ объектом как при наличии, так и при отсутствии внешних возмущающих воздействий в условиях априорной и текущей неопределенности.

Дата добавления: 2014-03-11; просмотров: 614; Нарушение авторских прав

Мы поможем в написании ваших работ!