
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Оптимизация цифровых регуляторов и компенсаторов многосвязной системы при невыполнении условия автономности
Вариант 2
Вариант 1
Процесс поиска оптимальных значений настроек основных регуляторов осуществляется в несколько этапов. На первом этапе выполняется расчет вектора 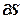 , на втором – осуществляется шаг по каждому настроечному параметру в направлении убывания критерия (4.41). Для вычисления
, на втором – осуществляется шаг по каждому настроечному параметру в направлении убывания критерия (4.41). Для вычисления 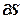 задаются начальные значения параметров цифровых регуляторов, при которых выполняется расчет
задаются начальные значения параметров цифровых регуляторов, при которых выполняется расчет 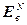 и
и 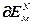 .
.
Вычисление вектора 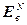 осуществляется путем расчета переходных процессов многосвязной системы (рис. 4.5) по разностным уравнениям в матричной форме:
осуществляется путем расчета переходных процессов многосвязной системы (рис. 4.5) по разностным уравнениям в матричной форме:
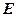 =
=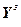 -
-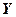 , (4.48)
, (4.48)
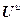 =
=
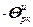 ,
,
 =
=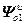
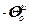 ,
,
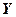 =
=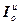
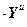 ,
,
где 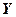 ,
,  ,
,  ,
, 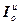 – см. в разделе 4.1.2;
– см. в разделе 4.1.2;
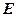 =[
=[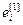 ,…,
,…,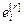 ]Т – вектор ошибки управления;
]Т – вектор ошибки управления;
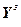 =[
=[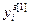 ,…,
,…,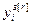 ]Т – вектор заданий;
]Т – вектор заданий;
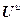 =
=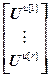 – блочный вектор;
– блочный вектор;
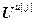 =[
=[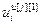 ,…,
,…,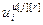 ]Т – вектор выходов j-го регулятора и компенсаторов, подключенных к его выходу; j=
]Т – вектор выходов j-го регулятора и компенсаторов, подключенных к его выходу; j=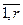 ;
;
 =
=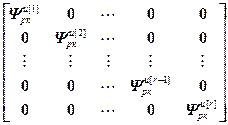 ,
,
 =
=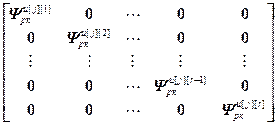 – блочные матрицы;
– блочные матрицы;
 =
=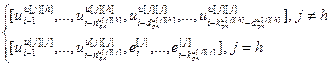 – матрица-строка переменных состояния j-го регулятора (j=h) или компенсатора (j≠h), подключенного к его выходу,
– матрица-строка переменных состояния j-го регулятора (j=h) или компенсатора (j≠h), подключенного к его выходу, 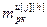 ; j, h=
; j, h=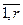 ;
;
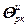 =
=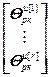 ,
,  =
=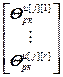 – блочные векторы;
– блочные векторы;
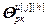 =[
=[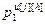 ,…,
,…,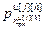 ,
,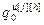 ,…,
,…,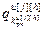 ]
]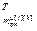 – вектор настроечных параметров j-го регулятора (j=h) или компенсатора (j≠h), подключенного к его выходу; j, h=
– вектор настроечных параметров j-го регулятора (j=h) или компенсатора (j≠h), подключенного к его выходу; j, h=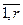 ;
;
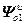 =
=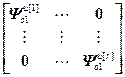 ,
, 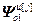 =
=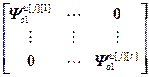 – блочные матрицы;
– блочные матрицы;
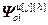 =[
=[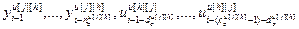 ]
]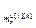 – матрица-строка переменных состояния основного или перекрестного канала, связывающего j-ое управляющее воздействие и h-ую управляемую величину;
– матрица-строка переменных состояния основного или перекрестного канала, связывающего j-ое управляющее воздействие и h-ую управляемую величину; 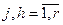 .
.
Расчет численных значений частных производных выходов регулируемых величин выполняется с помощью квазианалитических уравнений:
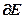 = –
= – , (4.49)
, (4.49)
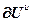 =
=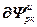
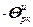 +
+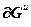 ,
,
 =
=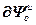
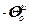 ,
,
 =
=
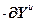 ,
,
где 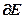 =
= – блочный вектор;
– блочный вектор;
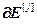 =[
=[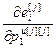 ,…,
,…, ,
,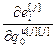 ,…,
,…,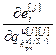 ]
]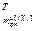 – вектор частных производных ошибки j-го выхода по настройкам j-го регулятора;
– вектор частных производных ошибки j-го выхода по настройкам j-го регулятора;  ;
;
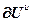 =
=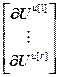 ,
, 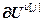 =
=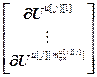 – блочные векторы;
– блочные векторы;
 =
= – вектор частных производных выходов j-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j=
– вектор частных производных выходов j-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j=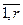 , h=
, h=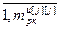 ;
;
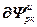 =
= ,
, 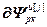 =
=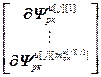 ,
,
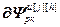 =
= – блочные матрицы и блочный вектор;
– блочные матрицы и блочный вектор;
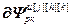 =
=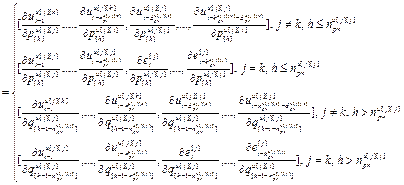
– матрица-строка частных производных переменных состояния выхода j-го регулятора (j=k) или компенсатора (j≠k), подключенного к его выходу, по h-ой настройке j-го регулятора, 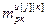 ; j, k
; j, k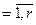 ,
, 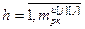 ;
;
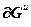 =
=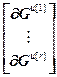 ,
, 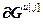 =
= – блочные векторы;
– блочные векторы;
 =
=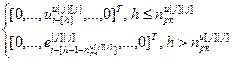 – вектор, все элементы которого равны нулю, кроме j-го, для расчета частных производных выходов j-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j
– вектор, все элементы которого равны нулю, кроме j-го, для расчета частных производных выходов j-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j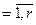 ,
, 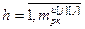 ;
;
 =
=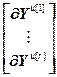 ,
, 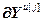 =
= – блочные векторы;
– блочные векторы;
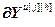 =
=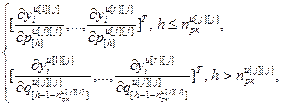 – вектор частных производных выходов основного и перекрестных каналов, связывающих j-ую управляемую величину со всеми управляющими величинами, по h-ой настройке j-го регулятора, r; j
– вектор частных производных выходов основного и перекрестных каналов, связывающих j-ую управляемую величину со всеми управляющими величинами, по h-ой настройке j-го регулятора, r; j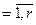 ,
, 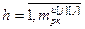 ;
;
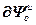 =
=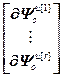 ,
, 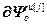 =
= ,
,
 =
=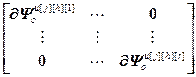 – блочные векторы и блочная матрица;
– блочные векторы и блочная матрица;
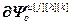 =[0,…,
=[0,…,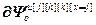 ,…,0] – блочная матрица-строка, элементами которой являются нулевые матрицы-строки (количество нулевых матриц-строк равно (r–1), каждая размерности
,…,0] – блочная матрица-строка, элементами которой являются нулевые матрицы-строки (количество нулевых матриц-строк равно (r–1), каждая размерности  ) и матрицы-строки вида:
) и матрицы-строки вида:
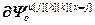 =
=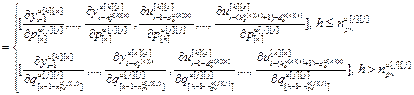 – матрица-строка частных производных переменных состояния выхода основного (k=x) или перекрестного (k≠x) каналов, связывающих k-ое управляющее воздействие и x-ую управляемую величину, по h-ой настройке j-го регулятора,
– матрица-строка частных производных переменных состояния выхода основного (k=x) или перекрестного (k≠x) каналов, связывающих k-ое управляющее воздействие и x-ую управляемую величину, по h-ой настройке j-го регулятора,  ; j, k, x
; j, k, x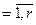 ,
, 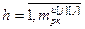 ;
;
 =
= – блочный вектор;
– блочный вектор;
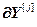 =
=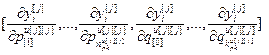
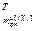 – вектор частных производных j-ой управляемой величины по настройкам j-го регулятора;
– вектор частных производных j-ой управляемой величины по настройкам j-го регулятора;  ;
;
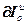 =
=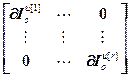 ,
, 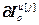 =
=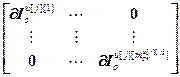 – блочные матрицы;
– блочные матрицы;
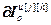 =[1,…,1] – единичная матрица-строка, r;
=[1,…,1] – единичная матрица-строка, r;
 ,
, 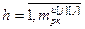 .
.
После проведения первого этапа оптимизации, на котором в результате решения систем уравнений (4.48) – (4.49) вычисляются в начале векторы 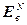 и
и 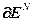 , а затем значения вектора
, а затем значения вектора 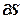 (4.47), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:
(4.47), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:
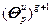 =(
=(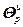 –
–
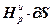 )g, (4.50)
)g, (4.50)
где g – номер итерации приближения к оптимуму;
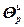 =
= – блочный вектор;
– блочный вектор;
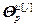 =
=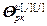 – вектор настроечных параметров j-го регулятора,
– вектор настроечных параметров j-го регулятора, 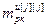 ;
;  ;
;
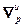 =
=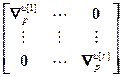 – блочная диагональная матрица;
– блочная диагональная матрица;
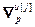 =
=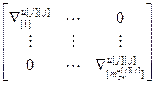 – диагональная матрица нормы градиента j-го критерия,
– диагональная матрица нормы градиента j-го критерия, 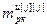 ´
´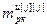 ;
;
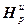 =
=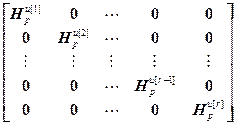 – блочная диагональная матрица;
– блочная диагональная матрица;
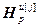 =
=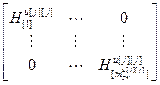 – диагональная матрица коэффициентов шага,
– диагональная матрица коэффициентов шага, 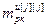
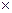
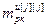 .
.
Для вычисления коэффициента шага воспользуемся алгоритмом, обеспечивающим высокую скорость достижения оптимума, который можно представить в матричной форме следующим образом:
diag[(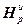 )g]=(
)g]=(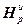 )g-1∙(
)g-1∙( )g, (4.51)
)g, (4.51)
где  =
=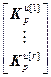 – блочный вектор;
– блочный вектор;
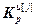 =[
=[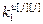 ,…,
,…,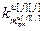 ]Т – вектор переменных коэффициентов по j-му каналу.
]Т – вектор переменных коэффициентов по j-му каналу.
Значение j-го элемента вектора 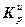 определяется выражением:
определяется выражением:

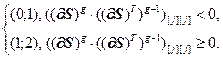 (4.52)
(4.52)
Норма градиента вычисляется с помощью зависимости:
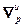 =(
=( )Т∙
)Т∙ . (4.53)
. (4.53)
где  =
= ,
,
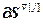 =
=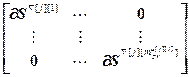 – блочные матрицы;
– блочные матрицы;  =
= – вектор частных производных j-го критерия по всем настройкам j-го регулятора; j=
– вектор частных производных j-го критерия по всем настройкам j-го регулятора; j=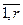 , h=
, h=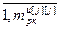 .
.
Момент окончания поиска оптимума определяется выполнением предварительно заданных условий:
 <
<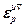 , (4.54)
, (4.54)
или
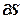 <
<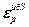 , (4.55)
, (4.55)
где  =[
=[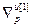 ,…,
,…,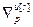 ]Т – вектор норм градиента всех критериев;
]Т – вектор норм градиента всех критериев; 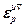 =[
=[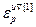 ,…,
,…,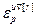 ]Т – вектор заданной точности расчета оптимальных значений настроек всех регуляторов при использовании условия (4.54);
]Т – вектор заданной точности расчета оптимальных значений настроек всех регуляторов при использовании условия (4.54);
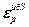 =
=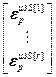 – блочный вектор;
– блочный вектор; 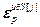 =[
=[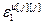 ,…,
,…,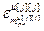 ]Т – вектор заданной точности расчета оптимальных значений настроек j-го регулятора при использовании условия (4.55); j=
]Т – вектор заданной точности расчета оптимальных значений настроек j-го регулятора при использовании условия (4.55); j=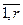 .
.
Для выполнения расчета по уравнениям (4.48) – (4.49) необходимо предварительно задаться начальными условиями:
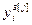 =
=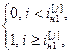 ,
,  , (4.56)
, (4.56)
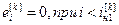 ,
,  , (4.57)
, (4.57)
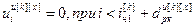 ,
, 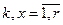 , (4.58)
, (4.58)
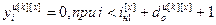 ,
, 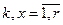 , (4.59)
, (4.59)
 ,
,  ,(4.60)
,(4.60)

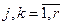 , (4.61)
, (4.61)
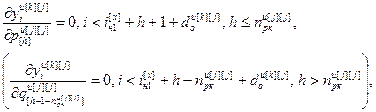
 , (4.62)
, (4.62)
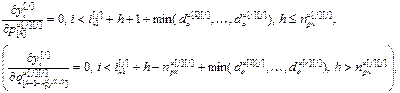
 , (4.63)
, (4.63)
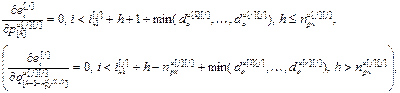
 , (4.64)
, (4.64)
где iн1[j]=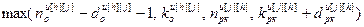 – значение номера такта, с которого начинается расчет переходного процесса по зависимостям (4.48) – (4.49);
– значение номера такта, с которого начинается расчет переходного процесса по зависимостям (4.48) – (4.49);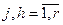 .
.
Анализ приведенного варианта позволяет сделать выводы относительно его достоинств и недостатков. К достоинствам относятся:
1. Анализ элементов вектора (4.40), (4.46) показывает зависимость управляемых величин от передаточных функций разных каналов и алгоритмов управления, т.е. полную их независимость (автономность) друг от друга. Благодаря этому настройка регуляторов является задачей скалярной оптимизации, что значительно упрощает и облегчает ее выполнение, и дает возможность независимой друг от друга, а, следовательно, и одновременной оптимизации управляющих алгоритмов ЦСУ на распределенных средствах цифровой вычислительной техники (ЦВТ);
2. Использование итерационных численных методов для оптимизации параметров управления только основных регуляторов АвЦСУ, а настройка компенсаторов перекрестных связей осуществляется в результате однократного расчета;
3. Анализ выражения (4.35) показывает, что при использовании первого подхода передаточные функции компенсаторов i-ой группы не зависят от передаточных функций основного и перекрестных каналов, оказывающих влияние на одну и туже i-ую управляемую величину. Это позволяет сделать вывод о том, что в случае нестационарности основного и перекрестных каналов, влияющих на одну и туже i-ую управляемую величину, не требуется проведения перенастройки компенсаторов i-ой группы.
Из приведенных достоинств следует, что главными преимуществами разработанного алгоритма являются малая потребность в использовании мощных и дорогостоящих средств ЦВТ и времени, затрачиваемого на оптимизацию алгоритмов управления АвЦСУ, за счет снижения количества уравнений и, следовательно, объема вычислений. Кроме того, облегчается настройка и обслуживание АвЦСУ.
Недостатком является специализация алгоритма на настройке управляющей части только АвЦСУ. Это сужает область его применения, снижая при этом функциональные возможности многомерной ЦСУ, работа которой основана на использовании только одного алгоритма оптимизации. Это приводит к невозможности использования соответствующего программного обеспечения для любых систем связанного управления и необходимости использования мощных дорогостоящих ЭВМ при наличии объекта большой размеренности (r>3).
Анализ выражения (4.46) показывает, что r-мерную ЦСУ (рис. 4.5) при выполнении условия автономности можно представить в виде совокупности r одномерных (одноконтурных) систем (рис. 4.7), каждая из которых включает соответствующий основной регулятор связанной системы (4.65) и эквивалентный объект с передаточной функцией (4.66):
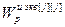 =
=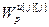 , (4.65)
, (4.65)
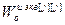 =
= +
+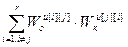 , j=
, j=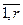 . (4.66)
. (4.66)

Рис. 4.7. Эквивалентная структурная схема системы
автономного управления r-мерным объектом
Сепаратные системы включают эквивалентные объекты, передаточные функции которых получаются из условия автономного управления. Поэтому при использовании данного варианта расчет основных регуляторов управляющей части системы сводится к задаче скалярной оптимизации в одноконтурной системе на основе разностных уравнений соответствующих эквивалентных объектов. Условие оптимальности при этом остается неизменным. С учетом вышесказанного динамику такой системы можно описать следующими разностными уравнениями в векторно-матричной форме:
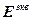 =
=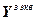 -
-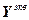 , (4.67)
, (4.67)
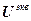 =
=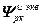
 ,
,
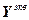 =
=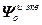
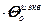 ,
,
где 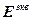 =
=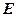 – вектор эквивалентной ошибки управления;
– вектор эквивалентной ошибки управления; 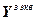 =
=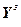 – вектор эквивалентных заданий;
– вектор эквивалентных заданий; 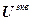 =[
=[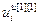 ,…,
,…,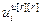 ]Т – вектор эквивалентных управляющих воздействий;
]Т – вектор эквивалентных управляющих воздействий;
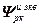 =
=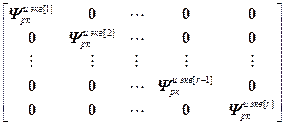 – блочная матрица;
– блочная матрица;
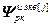 =[
=[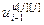 ,…,
,…,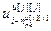 ,
,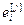 ,…,
,…, ] – матрица-строка переменных состояния j-го эквивалентного регулятора,
] – матрица-строка переменных состояния j-го эквивалентного регулятора, 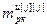 ;
;  ;
;
 =
=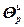 – вектор настроечных параметров всех регуляторов;
– вектор настроечных параметров всех регуляторов;
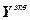 =
=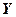 – вектор эквивалентных управляемых величин;
– вектор эквивалентных управляемых величин;
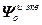 =
=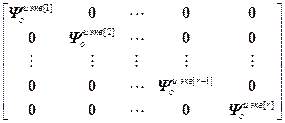 – блочная матрица;
– блочная матрица;
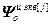 =[
=[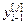 ,…,
,…,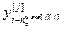 ,
,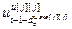 ,…,
,…,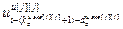 ] – матрица-строка переменных состояния j-го эквивалентного ОУ,
] – матрица-строка переменных состояния j-го эквивалентного ОУ, 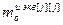 ;
;  ;
;
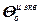 =
=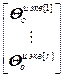 – блочный вектор;
– блочный вектор;
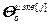 =[
=[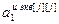 ,…,
,…,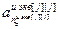 ,
,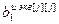 ,…,
,…, ]T – вектор параметров модели j-го эквивалентного ОУ,
]T – вектор параметров модели j-го эквивалентного ОУ, 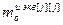 ;
;
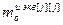 =
=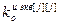 +
+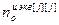 +1 – число переменных состояния эквивалентного ОУ;
+1 – число переменных состояния эквивалентного ОУ;
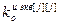 ,
, 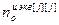 – порядки числителя и знаменателя дискретной передаточной функции эквивалентного ОУ;
– порядки числителя и знаменателя дискретной передаточной функции эквивалентного ОУ;  – число тактов запаздывания эквивалентного ОУ;
– число тактов запаздывания эквивалентного ОУ;  .
.
Расчет численных значений частных производных в векторно-матричной форме:
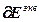 =-
=-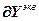 , (4.68)
, (4.68)
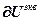 =
=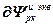
 +
+ ,
,
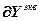 =
=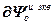
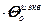 ,
,
где 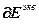 =
=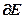 – вектор частных производных всех эквивалентных ошибок по всем настройкам эквивалентных регуляторов;
– вектор частных производных всех эквивалентных ошибок по всем настройкам эквивалентных регуляторов;
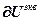 =
=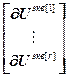 – блочный вектор;
– блочный вектор;
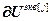 =[
=[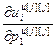 ,…,
,…,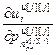 ,
, ,…,
,…,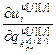 ]Т – вектор частных производных выхода j-го эквивалентного регулятора по его настройкам,
]Т – вектор частных производных выхода j-го эквивалентного регулятора по его настройкам, 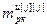 ;
;  ;
;
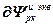 =
=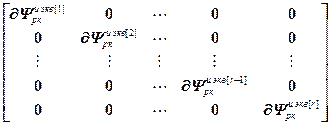 ,
,
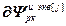 =
=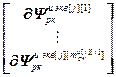 – блочная матрица и блочный вектор;
– блочная матрица и блочный вектор;
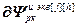 =
=
= – матрица-строка частных производных переменных состояния j-го эквивалентного регулятора по его h-ой настройке,
– матрица-строка частных производных переменных состояния j-го эквивалентного регулятора по его h-ой настройке, 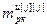 ;
; 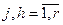 ;
;
 =
= – блочный вектор;
– блочный вектор;
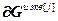 =(
=(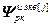 )T – вектор дополнительных слагаемых для расчета частных производных j-го эквивалентного регулятора;
)T – вектор дополнительных слагаемых для расчета частных производных j-го эквивалентного регулятора;  ;
;
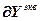 =
= – вектор частных производных управляемых величин по всем настройкам эквивалентных регуляторов,
– вектор частных производных управляемых величин по всем настройкам эквивалентных регуляторов, 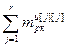 ;
;
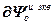 =
=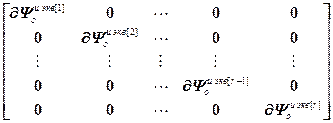 ,
,
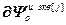 =
= – блочная матрица и блочный вектор;
– блочная матрица и блочный вектор;
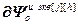 =
=
=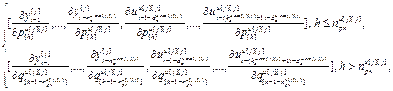 – блочная матрица матрица-строка частных производных переменных состояния выхода j-го эквивалентного канала по h-ой настройке j-го эквивалентного регулятора,
– блочная матрица матрица-строка частных производных переменных состояния выхода j-го эквивалентного канала по h-ой настройке j-го эквивалентного регулятора, 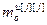 ;
; 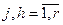 .
.
Расчет оптимальных значений настроек основных регуляторов будет проводиться по тем же зависимостям (4.50) – (4.55), что и в первом алгоритме.
Для выполнения расчета выражений (4.67) – (4.68) необходимо предварительно задаться начальными условиями:
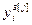 =
= ,
,  , (4.69)
, (4.69)
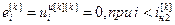 ,
,  , (4.70)
, (4.70)
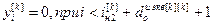 ,
,  , (4.71)
, (4.71)
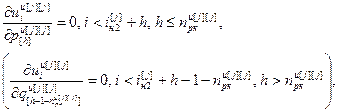
 , (4.72)
, (4.72)
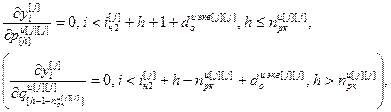
 , (4.73)
, (4.73)
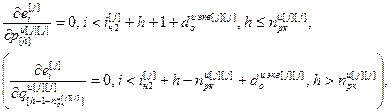
 , (4.74)
, (4.74)
где iн2[j]=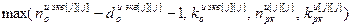 – значение номера такта, с которого начинается расчет переходного процесса по зависимостям (4.67) – (4.68);
– значение номера такта, с которого начинается расчет переходного процесса по зависимостям (4.67) – (4.68);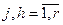 .
.
Главными преимуществом алгоритма является возможность использования значительно менее мощных средств ЦВТ с относительно небольшими объемами оперативной памяти по сравнению с предыдущим алгоритмом, особенно при наличии объекта большой размерности (r>3). Во-вторых, уменьшение времени, затрачиваемого на оптимизацию алгоритмов управления АвЦСУ. Кроме того, значительно облегчается настройка и обслуживание АвЦСУ.
Недостатками алгоритма являются:
1. Необходимость использования верхнего уровня АСУ (рабочая станция, ЭВМ), возможности которой позволяют установить и использовать пакет прикладных программ для расчета передаточных функций эквивалентных объектов (при использовании первого подхода для расчет компенсаторов перекрестных связей) и компенсаторов перекрестных связей;
2. Возможность использования данного алгоритма для настройки управляющей части только АвЦСУ;
Ограничения на физическую реализуемость автономных компенсаторов перекрестных связей [12] приводят к невозможности использования критерия автономности при синтезе связанной системы управления. Кроме того, автономизация в ряде случаев [35] с последующей оптимизацией регуляторов не всегда обеспечивает оптимум всей системы. Поэтому второй подход при синтезе связанной системы формулируется в виде требования экстремизировать функционал, зависящий от всех управляемых величин с учетом того, что на каждую из них оказывают влияние все управляющие воздействия. В этом случае синтез основан на использовании численных методов оптимизации настроек не только регуляторов, но и компенсаторов перекрестных связей.
В любых системах несвязанного или связанного управления, кроме автономных, теоретически не достигается полная компенсация внутренних динамических связей. Вследствие этого на каждую из управляемых величин оказывается влияние со стороны всех управляющих и компенсирующих алгоритмов. Таким образом, настройка регуляторов и компенсаторов многомерных ЦСУ данного класса в соответствии с приведенным критерием (4.37) оказывается задачей векторной оптимизации, решение которой вызывает значительные трудности и требует больших временных затрат.
Рассмотрим алгоритм оптимизации регуляторов связанной неавтономной ЦСУ для случая, когда настройки компенсаторов определены заранее [3]. Это дает возможность с одной стороны избежать излишнего усложнения в описании, а с другой стороны позволяет довольно просто перейти к алгоритмам одновременной оптимизации регуляторов и компенсаторов неавтономной ЦСУ и оптимизации регуляторов несвязанной ЦСУ многомерным объектом.
Существует несколько подходов для решения задач векторной оптимизации [9]. Воспользуемся методом свертки:
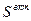 =
=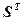 ∙
∙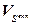 , (4.75)
, (4.75)
где 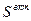 – суммарный критерий;
– суммарный критерий;
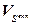 =[
=[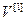 ,…,
,…,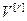 ]Т – вектор весовых коэффициентов каждой управляемой величины:
]Т – вектор весовых коэффициентов каждой управляемой величины:
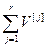 =1. (4.76)
=1. (4.76)
Критерий 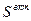 , представленный в виде суммы квадратичных функций вектора S, ограниченных снизу, по этой причине также будет являться квадратичной функцией ограниченной снизу. В этом случае необходимым и достаточным условием экстремума является следующее равенство:
, представленный в виде суммы квадратичных функций вектора S, ограниченных снизу, по этой причине также будет являться квадратичной функцией ограниченной снизу. В этом случае необходимым и достаточным условием экстремума является следующее равенство:
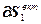 =
=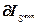 ·
·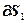 =0, (4.77)
=0, (4.77)
где 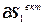 =
=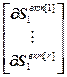 – блочный вектор;
– блочный вектор;
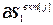 =[
=[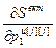 ,…,
,…,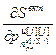 ,
,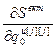 ,…,
,…,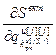 ]
]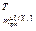 – вектор частных производных критерия S вкт по всем оптимизируемым настройкам j-го регулятора; j=
– вектор частных производных критерия S вкт по всем оптимизируемым настройкам j-го регулятора; j=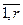 ;
;
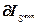 =
=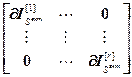 ,
,
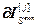 =
=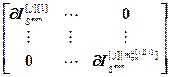 – блочные матрицы;
– блочные матрицы;
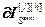 =
=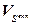 – матрица-строка;
– матрица-строка;  ,
, 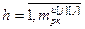 .
.
Значение вектора 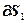 определяется из выражения:
определяется из выражения:
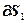 =2·
=2·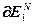
 , (4.78)
, (4.78)
где 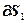 =
=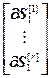 ,
, 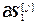 =
= – блочные векторы;
– блочные векторы;
 =
=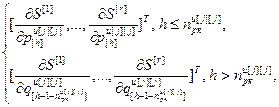 – вектор частных производных всех критериев по h-ой настройке j-го регулятора, r; j=
– вектор частных производных всех критериев по h-ой настройке j-го регулятора, r; j=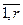 , h=
, h=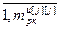 ;
;
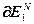 =
=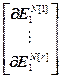 ,
, 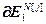 =
= ,
,
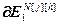 =
=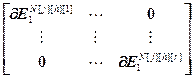 – блочные векторы и блочная матрица;
– блочные векторы и блочная матрица;
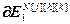 =
= – матрица-строка значений частной производной k-ой ошибки управления по h-ой настройке j-го регулятора, Nв; j, k=
– матрица-строка значений частной производной k-ой ошибки управления по h-ой настройке j-го регулятора, Nв; j, k=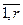 ,
,
h=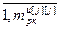 .
.
Отыскание оптимальных значений настроек основных регуляторов осуществляется в несколько этапов. На первом этапе задаются начальные значения параметров алгоритмов управления, при которых выполняется расчет переходных процессов замкнутой многомерной ЦСУ и частных производных (4.77).
Расчет переходных процессов замкнутой связанной ЦСУ в ходе решения задачи оптимизации ведется с учетом как основных, так и перекрестных связей объекта с помощью разностных уравнений:
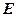 =
=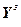 -
-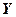 ,
,
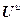 =
=
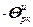 ,
,
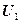 =
=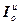
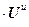 , (4.79)
, (4.79)
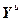 =
=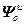
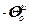 ,
,
 =
=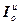
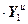 ,
,
где 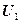 =[
=[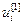 ,…,
,…,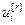 ]Т – вектор управляющих воздействий на объект управления.
]Т – вектор управляющих воздействий на объект управления.
Расчет численных значений частных производных выходов регуляторов, компенсаторов, основных и перекрестных каналов управлений, управляющих воздействий и управляемых величин осуществляется по уравнениям:
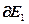 =-
=-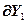 ,
,
 =
=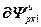
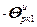 +
+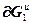 ,
,
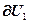 =
=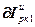
 , (4.80)
, (4.80)
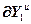 =
=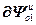
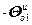 ,
,
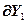 =
=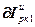
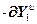 ,
,
где 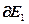 =
= ,
, 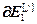 =
=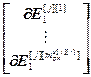 – блочные векторы;
– блочные векторы;
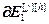 =
=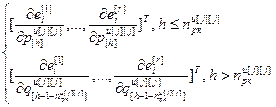 – вектор частных производных всех ошибок управления по h-ой настройке j-го регулятора, r;
– вектор частных производных всех ошибок управления по h-ой настройке j-го регулятора, r;  ,
, 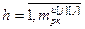 ;
;
 =
=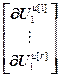 ,
, 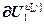 =
=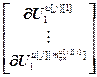 ,
,
 =
=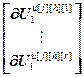 – блочные векторы;
– блочные векторы;
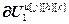 =
=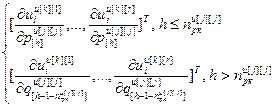 – вектор частных производных выходов k-го регулятора или компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j, k=
– вектор частных производных выходов k-го регулятора или компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j, k=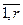 , h=
, h=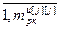 ;
;
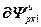 =
=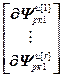 ,
, 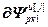 =
= ,
,
 =
=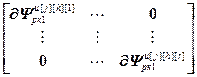 ,
,
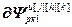 =
=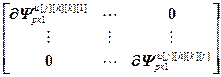 – блочные векторы и блочные матрицы;
– блочные векторы и блочные матрицы;
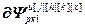 =
=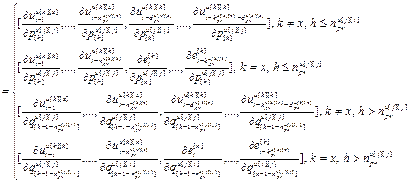 – матрица-строка частных производных переменных состояния k-го регулятора (k=x) или компенсатора (k≠x), подключенного к его выходу, по h-ой настройке j-го регулятора,
– матрица-строка частных производных переменных состояния k-го регулятора (k=x) или компенсатора (k≠x), подключенного к его выходу, по h-ой настройке j-го регулятора, 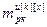 ; j, k, x
; j, k, x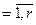 ,
, 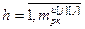 ;
;
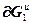 =
=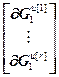 ,
, 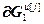 =
=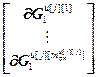 – блочные векторы;
– блочные векторы;
 =
= – блочный вектор, элементы которого являются нулевыми векторами (количество нулевых векторов равно (r-1), каждый размерности r), кроме j-го (k=j) вектора вида:
– блочный вектор, элементы которого являются нулевыми векторами (количество нулевых векторов равно (r-1), каждый размерности r), кроме j-го (k=j) вектора вида:
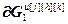 =
=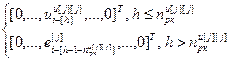 – вектор, элементы которого равны нулю кроме j-го, являющегося h-ой переменной состояния j-го регулятора, для расчета значений частных производных выходов k-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j, k
– вектор, элементы которого равны нулю кроме j-го, являющегося h-ой переменной состояния j-го регулятора, для расчета значений частных производных выходов k-го регулятора и компенсаторов, подключенных к его выходу, по h-ой настройке j-го регулятора, r; j, k 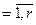 ,
, 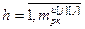 ;
;
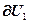 =
=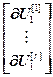 ,
, 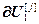 =
=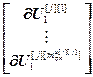 – блочные векторы;
– блочные векторы;
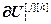 =
=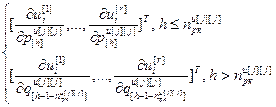 – вектор частных производных выходов всех управляющих воздействий по h-ой настройке j-го регулятора, r;
– вектор частных производных выходов всех управляющих воздействий по h-ой настройке j-го регулятора, r;  ,
, 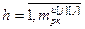 ;
;
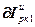 =
=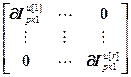 ,
,
 =
=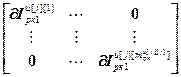 – блочные матрицы;
– блочные матрицы;
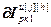 =
=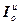 – матрица суммирования;
– матрица суммирования;  ,
, 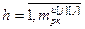 ;
;
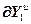 =
=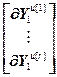 ,
, 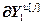 =
=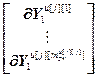 ,
,  =
=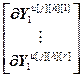 – блочные векторы;
– блочные векторы;
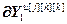 =
= – вектор частных производных выходов основного и перекрестных каналов, связывающих k-ое управляющее воздействие со всеми управляемыми величинами, по h-ой настройке j-го регулятора, r; j, k
– вектор частных производных выходов основного и перекрестных каналов, связывающих k-ое управляющее воздействие со всеми управляемыми величинами, по h-ой настройке j-го регулятора, r; j, k 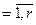 ,
, 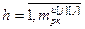 ;
;
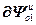 =
=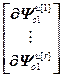 ,
,  =
=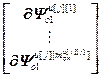 ,
,
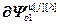 =
=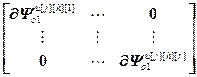 ,
,
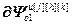 =
=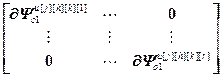 – блочные векторы и блочные матрицы;
– блочные векторы и блочные матрицы;
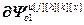 = =
= =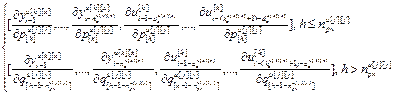 – матрица-строка частных производных переменных состояния основного (k=x) или перекрестного (k≠x) каналов, связывающего k-ое управляющее воздействие и x-ую управляющую величину, по h-ой настройке j-го регулятора,
– матрица-строка частных производных переменных состояния основного (k=x) или перекрестного (k≠x) каналов, связывающего k-ое управляющее воздействие и x-ую управляющую величину, по h-ой настройке j-го регулятора,  ; j, k, x
; j, k, x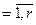 ,
, 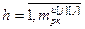 ;
;
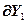 =
= ,
, 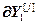 =
=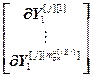 – блочные векторы;
– блочные векторы;
 =
=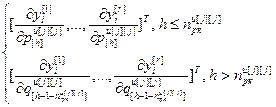 – вектор частных производных выходов всех управляемых величин по h-ой настройке j-го регулятора, r;
– вектор частных производных выходов всех управляемых величин по h-ой настройке j-го регулятора, r;  ,
, 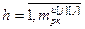 .
.
После проведения первого этапа оптимизации, на котором в результате решения систем уравнений (4.79) – (4.80) вычисляются в начале векторы 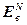 и
и 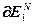 , а затем значения векторов
, а затем значения векторов 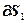 (4.78) и
(4.78) и 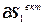 (4.77), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:
(4.77), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:
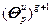 =(
=(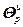 –
–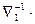
 )g, (4.81)
)g, (4.81)
где g – номер итерации приближения к оптимуму;
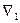 – норма градиента.
– норма градиента.
Для вычисления коэффициента шага используются следующие выражения, записанные в матричной форме:
diag[( )g]=(
)g]=( )g-1∙(
)g-1∙( )g. (4.82)
)g. (4.82)
Значение j-го элемента вектора  определяется выражением:
определяется выражением:

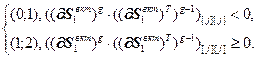 (4.83)
(4.83)
Норма градиента вычисляется с помощью зависимости:
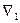 =
= . (4.84)
. (4.84)
Момент окончания поиска оптимума определяется выполнением некоторых предварительно заданных условий:
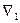 <
<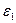 , (4.85)
, (4.85)
или
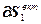 <
<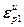 , (4.86)
, (4.86)
где 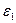 – заданная точность расчета точки экстремума при использовании условия (4.85);
– заданная точность расчета точки экстремума при использовании условия (4.85);
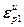 =
=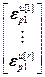 – блочный вектор;
– блочный вектор; 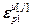 =[
=[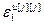 ,…,
,…,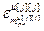 ]Т – вектор заданной точности расчета оптимальных значений настроек j-го регулятора при использовании условия (4.86),
]Т – вектор заданной точности расчета оптимальных значений настроек j-го регулятора при использовании условия (4.86), 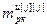 ; j=
; j=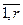 .
.
Для выполнения расчета выражений (4.79) – (4.80) необходимо предварительно задаться начальными условиями:
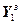 =
= , (4.87)
, (4.87)
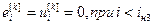 ,
,  , (4.88)
, (4.88)
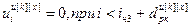 ,
, 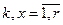 , (4.89)
, (4.89)
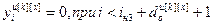 ,
,
| <== предыдущая страница | | | следующая страница ==> |
| Оптимизация цифровых регуляторов при выполнении условия автономности | | | Алгоритм синтеза многосвязных автономно-инваринатных ЦСУ |
Дата добавления: 2014-03-11; просмотров: 598; Нарушение авторских прав

Мы поможем в написании ваших работ!