Оптимизация цифровых регуляторов при выполнении условия автономности

После расчета компенсаторов из условия автономности в многомерной ЦСУ выполняется оптимизация основных регуляторов. Оптимизация может проводиться с использованием различных критериев (см. разд. 2.2). Наиболее часто для этих целей применяется квадратичная интегральная оценка, аналогом которой при построении дискретных систем управления является сумма квадратов ошибок управления:

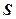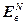=, (4.41)

где 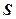=[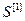,…,]^Т – вектор критериев каждой управляемой величины;

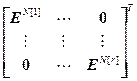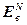=, =– блочная матрица и блочный вектор;

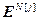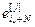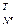=[,…,]– вектор дискретных значений ошибок для j-ой управляемой величины;

N^в=N+1 – объем выборки дискретных значений ошибок на период времени переходного процесса j-ой управляемой величины;

– индексы такта квантования.

Для решения задачи синтеза основных регуляторов управляющей части автономной системы, необходимо проанализировать уравнение (4.29), описывающее поведение многомерной ЦСУ, которое с учетом (4.30) принимает вид:

y=(I+R)^-1·R·y^з, (4.42)

где R=W_о^u·W_к^u·W_р^u.

При выполнении условия автономности матрица R является диагональной, элементы которой исходя из (4.30) и (4.31) равны:

R==

(4.43)

Поскольку:

(I+R)^-1==

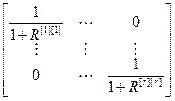=, то (4.44)

(I+R)^-1·R==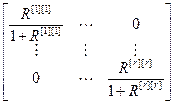

(4.45)

Отсюда уравнение (4.42), определяющее функциональную зависимость выходов объекта от входов системы, примет вид:

=

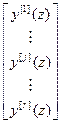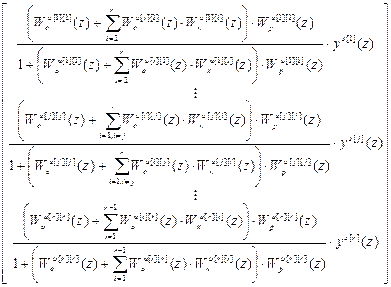=.(4.46)

Анализ (4.46) показывает, что в автономной ЦСУ (АвЦСУ) каждая из управляемых величин 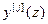является функцией только соответствующих задающего воздействия и регулятора 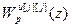, поскольку передаточные функции компенсаторов (см. раздел 4.2.1) и каналов объекта определены. Таким образом, настройка регуляторов в соответствии с приведенным критерием (4.41) оказывается задачей скалярной оптимизации, т.к. каждый элемент вектора S зависит от настроечных параметров только одного регулятора. Учитывая это обстоятельство, необходимое условие экстремума примет вид:

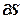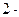
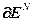
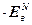==0, (4.47)

где 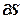=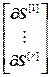– блочный вектор;

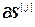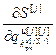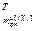=[,…,,,…,]– вектор частных производных j-го критерия по всем настройкам j-го регулятора; j=;

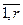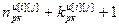=– число настроечных параметров регуляторов (i=j) или компенсаторов (i≠j) перекрестных связей; .

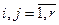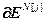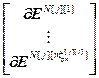=, =– блочная матрица и блочный вектор;

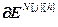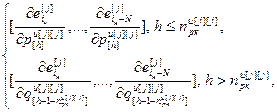=– матрица-строка численных значений частной производной j-ой ошибки управления по h-ой настройке j-го регулятора, N^в; j=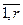, h=.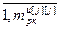

Как ранее было сказано, возможны два варианта оптимизации настроек регуляторов. Рассмотрим первый вариант, при котором проводится одновременная параметрическая оптимизация всех регуляторов на основе моделей основных и перекрестных каналов.

Дата добавления: 2014-03-11; просмотров: 538; Нарушение авторских прав

Мы поможем в написании ваших работ!