Разработка дискретной динамической модели объекта

Глава 2. СИНТЕЗ ЦИФРОВОЙ МНОГОСВЯЗНОЙ СИСТЕМЫ УПРАВЛЕНИЯ ПРОЦЕССОМ ПОЛУЧЕНИЯ АММИАКА

Контрольные вопросы

4.3.1. Привести примеры многомерных технологических объектов. Почему применение одноконтурных систем не обеспечивает высокого качества управления такими объектами?

4.3.2. Какие структурные связи между параметрами могут иметь объекты?

4.3.3. Составить систему разностных уравнений многомерного объекта Р-канонической структуры.

4.3.4. Как получить дискретные передаточные функции для основных, перекрестных и каналов возмущений из разностных уравнений?

4.3.5. Чем удобно использование векторно-матричной формы описания многомерного объекта?

4.3.6. Составить систему матричных уравнений многомерного объекта?

4.3.7. Чем определяется число переменных состояния в дискретном уравнении модели объекта?

4.3.8. Как проводится параметрическая идентификация по каналам управления и возмущения?

4.3.9. Какие подходы существуют при синтезе управляющей части многомерной ЦСУ?

4.3.10. На каких принципах основаны синтез компенсаторов перекрестных связей и возмущений?

4.3.11. Описать связанную многомерную ЦСУ векторно-матричными уравнениями.

4.3.12. Какое условие автономности для многомерной системы управления?

4.3.13. Как рассчитываются перекрестные компенсаторы при условии автономности?

4.3.14. Какие два способа расчета перекрестных компенсаторов многомерной системы?

4.3.15. Записать квадратичный критерий оптимизации настроек цифровых регуляторов в дискретной форме для многомерной системы.

4.3.16. Почему задача оптимизации настроек цифровых регуляторов при выполнении условия автономности сводится к скалярной?

4.3.17. Из каких этапов состоит процесс поиска оптимальных настроек цифровых регуляторов?

4.3.18. Записать систему разностных уравнений в матричной форме многосвязной системы управления.

4.3.19. Как определяется момент окончания поиска оптимальных настроек?

4.3.20. Какие уравнения описывают эквивалентную схему автономной многосвязной системы?

4.3.21. Почему возрастает размерность задачи оптимизации параметров управляющей части системы при невыполнении условия автономности?

4.3.22. Квадратичный критерий оптимизации при невыполнении условия автономности.

4.3.23. В каких случаях необходимо использование СКЦСУ?

4.3.24. Какие варианты структурных схем СКЦСУ вы знаете?

4.3.25. Вывод зависимостей для расчета автономных и инвариантных компенсаторов перекрестных связей и возмущений для каждого из вариантов СКЦСУ (общие зависимости и частные).

4.3.26. Эквивалентное представление СКЦСУ при выполнении условий автономности и/или инвариантности.

4.3.27. Алгоритм синтеза (адаптации) многомерной ЦСУ.

Как отмечалось выше, целью технологического процесса синтеза аммиака, протекающего в четырехполочном реакторе аксиального типа, является получение газообразного аммиака с заданной концентрацией на выходе из реактора. В промышленных условиях, ввиду достаточно большой инерционности концентрации, а так же из-за значительных трудностей при ее измерении непосредственно в слоях катализатора реактора, процесс проводят путем стабилизации температуры в регламентных границах по слоям за счет изменения степени открытия заслонок на байпасных потоках.

В результате проведенных промышленных экспериментов установлено, что изменение степени открытия заслонки на байпасном потоке оказывает влияние на температуру как в соответствующем, так и в ниже лежащих слоях, кроме того, на температуру значительное влияние оказывают концентрация аммиака, концентрация инертных примесей и соотношения реагентов азотоводородной смеси.

Отсюда с позиции управления данный процесс является объектом со взаимосвязанными параметрами. Топология этих взаимосвязей, представлена на структурной схеме (рис. 2.1):

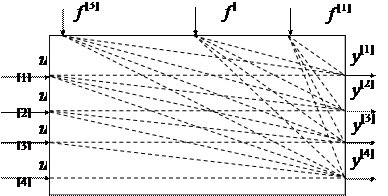
Рис 2.1. Структурная схема объекта: u^[1] ÷ u^[4] – степени открытия заслонок на байпасных потоках (управляющие параметры); y^[1] ÷ y^[4] – температура в слоях катализатора (управляемые параметры); f ^[1], f ^[2], f ^[3] ÷ концентрация аммиака, инертных газов и соотношение водород/азот (возмущающие воздействия).

Динамика каналов объекта управления описана конечно- разностными уравнениями [85]:

,

,

,

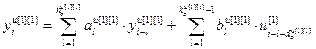(2.1)

,

,

,

,

.

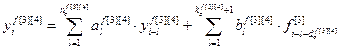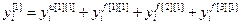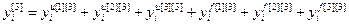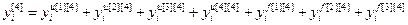Используя на основе переменной индексации универсальную запись разностного уравнения, дискретную модель объекта можно представить в виде:

,

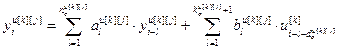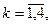
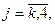
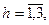
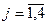, , (2.2)

, .

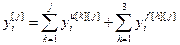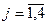Применяя оператор сдвига z, уравнения связи по каналам описываются с использованием дискретных передаточных функций W(z):

y^u[k][j](z)=W_о^u[k][j](z) · u^[k](z), ,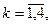

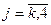y ^{f [h][j]}(z)=W_о^{f [h][j]}(z) ·f ^[h](z), 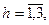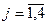, (2.3)

, ,

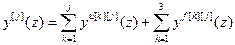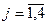где u^[k](z) – управляющее воздействие; – выход объекта; y^u[k][j](z) – выход по основному (k=j) или перекрестному (k≠j) каналу; f ^[h](z) – внешнее контролируемое возмущение; 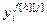– температура по каналу возмущения; 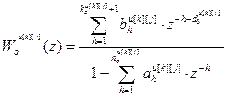− дискретная передаточная функция по основному, (k=j) или перекрестному (k≠j) каналу объекта управления,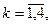 ; 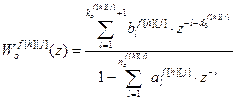− дискретная передаточная функция по каналу возмущения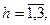 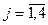; 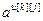, , 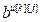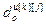− параметры и число тактов запаздывания разностного уравнения основного или перекрестного канала объекта управления; 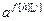, , 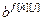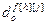− параметры и число тактов запаздывания разностного уравнения по каналу возмущения; , – порядки полиномов; i –индекс такта квантования; k – номер входа (номер байпасного потока); h – номер возмущения (концентрация аммиака, инертных газов, соотношение водорода и азота).

Запишем систему уравнений (2.3) в векторно-матричной форме:

y=W_о^u·u+W_о^f·f, (2.4)

где y=[y^[1](z),…,y^[4](z)]^Т – вектор выходов ОУ; и=[и^[1](z),…,и^[4](z)]^Т – вектор управляющих воздействий; f =[f ^[1](z), f ^[2](z), f ^[3](z)]^Т – вектор возмущений; W_о^u – треугольная матрица дискретных передаточных функций объекта по основным и перекрестным каналам, 44; W_о^f– матрица дискретных передаточных функций ОУ по каналам возмущений, 43;

;.

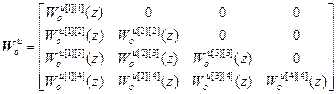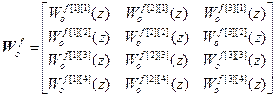Разработана дискретная динамическая модель многосвязного объекта (2.4), отличающаяся от известных тем, что учитывает одностороннее (несимметричное) влияние степени открытия заслонок на байпасных потоках на температуру в нижележащих слоях катализатора, а так же влияние на температуру в каждом слое возмущающих воздействий: концентрации аммиака, инертных примесей и состав азотоводородной смеси.

Анализ структуры взаимосвязей объекта позволяет сделать вывод, что добиться существенного повышение качества управления только лишь путем использования существующих на сегодняшний день на производствах аммиака одноконтурных систем, не учитывающих взаимного влияния между параметрами объекта, задача достаточно сложная. Одним из вариантов решения данной задачи является синтез многосвязной системы управления.

Дата добавления: 2014-03-11; просмотров: 565; Нарушение авторских прав

Мы поможем в написании ваших работ!