Разработка структуры и математическое описание многосвязной системы управления

Разработка управляющей части системы

Получение высокого качества управления многосвязными объектами при наличии внешних возмущений заключается в развязывании внутренних перекрестных каналов между выходными величинами и компенсации влияния возмущающих воздействий путем создания систем связно-комбинированого управления, вводя в них дополнительные внешние компенсирующие связи между регуляторами. Отсюда с целью повышения качества управления температурой в слоях колонны синтеза аммиака разработана структура 4-х мерной цифровой связно-комбинированной системы регулирования (СКЦСУ) [84,93,131] (рис 2.2):

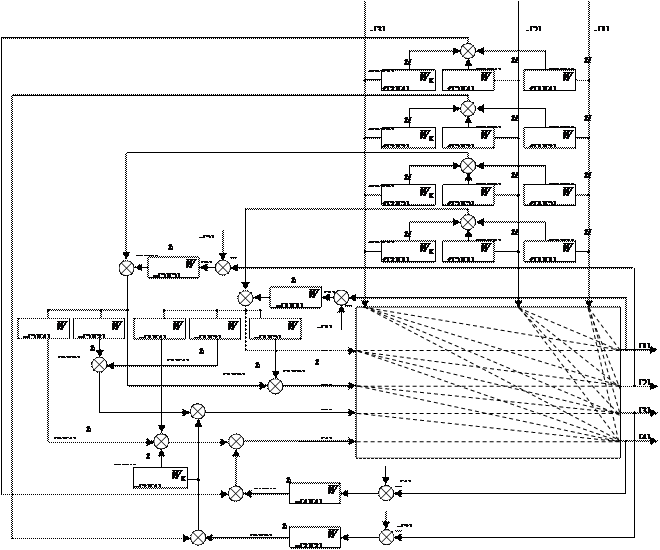
Рис. 2.2. Структурная схема СКЦСУ.

Поведение СКЦСУ описывается системой уравнений в векторно-матричной форме:

е=y^з-y,

u^u=W_р^u·е,

u=W_к^u·(u^u+W_к^f·f), (2.5)

y=W_о^u·u+W_o^f·f,

где е=[е^[1](z),…,е^[4](z)]^Т – вектор ошибок управления; y^з=[y^з[1](z),…,y^з[4](z)]^Т – вектор заданий; y=[y^[1](z),…,y^[4](z)]^Т – вектор выходов ОУ; и^u=[и^u[1][1](z),…,и^u[4][4](z)]^Т – вектор выходов основных регуляторов; и=[и^[1](z),…,и^[4](z)]^Т – вектор управляющих воздействий; f =[f ^[1](z), f ^[2](z), f ^[3](z)]^Т – вектор возмущений; W_р^u – диагональная матрица дискретных передаточных функций регуляторов, 4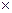4; W_к^u – матрица дискретных передаточных функций компенсаторов перекрестных связей, 4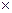4; W_о^f– матрица дискретных передаточных функций ОУ по каналам возмущений, 4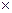3; W_к^f – матрица дискретных передаточных функций компенсаторов возмущений, 4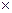3;

;

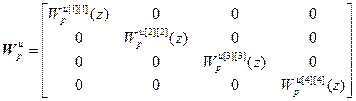W_р^u[i][j](z) {W_к^u[i][j](z)}={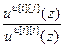}==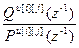– дискретная передаточная функция регулятора (i=j) или компенсатора (i≠j); 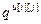, , 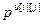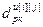– параметры дискретной передаточной функции регулятора (i=j) или компенсатора (i≠j); 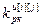, 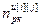– порядки числителя и знаменателя дискретной передаточной функции регулятора (i=j) или компенсатора (i≠j); u^u[i][j](z) – выходы регуляторов (i=j) и компенсаторов (i≠j); i, j=;

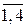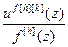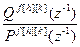
W_к^f[h][k](z)=== 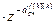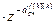– дискретная передаточная функция компенсатора возмущения; u ^{f [h][k]}(z) – выход компенсатора возмущения; 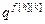, , 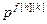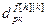– параметры дискретной передаточной функции компенсатора возмущений; , 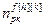– порядки числителя и знаменателя дискретных передаточных функций компенсаторов возмущений; h=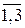, k=.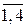

Выполнив преобразования над уравнениями системы (2.5) получим:

y=(I+W_о^u·W_к^u·W_р^u)^-1·W_о^u·W_к^u·W_р^u·y^з+(I+W_о^u·W_к^u·W_р^u)^-1·(W_о^u·W_к^u·W_к^f+W_o^f)·f, (2.6)

где I – единичная матрица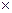, 44.

Уравнение (2.6) позволяет определить функциональную зависимость выходов ОУ (элементов y) от входов системы (элементов y^з и f).

Анализ выражения (2.6) позволяет сформулировать условия автономности и инвариантности. Условие автономности выполняется, если матрица (I+W_о^u·W_к^u·W_р^u) – диагональная, условие инвариантности выполняется, если второе слагаемое (2.6) обращается в нуль:

W_о^u·W_к^u·W_к^f+W_o^f=0. (2.7)

В общем случае, расчет управляющей части многомерной цифровой системы управления с использованием принципов автономно-инвариантного управления выполняется в следующей последовательности [86]:

1. Синтез цифровых компенсаторов перекрестных связей из условия автономности;

2. Расчет передаточных функций эквивалентных объектов;

3. Расчет параметров основных регуляторов по передаточным функциям эквивалентных объектов;

4. Расчет параметров компенсаторов возмущений из условия инвариантности.

Рассмотрим этапы синтеза цифровой системы управления.

Дата добавления: 2014-03-11; просмотров: 559; Нарушение авторских прав

Мы поможем в написании ваших работ!