Синтез компенсаторов перекрестных связей из условия автономности

Для выполнения первого этапа алгоритма рассмотрим систему связанного управления (рис. 2.3):

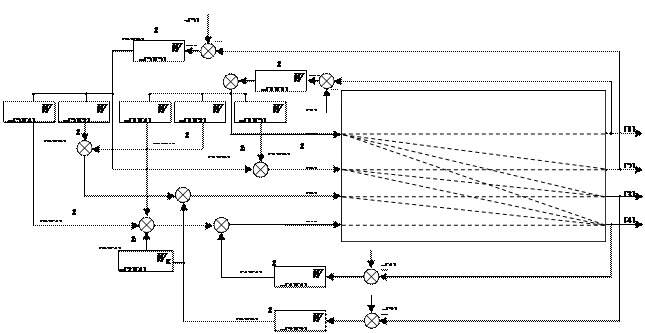
Рис. 2.3. Структурная схема связанной цифровой системы управления.

Поведение системы описано уравнением в векторно-матричной форме:

y=(I+W_о^u·W_к^u·W_р^u)^-1·W_о^u·W_к^u·W_р^u·y^з. (2.8)

Так как I – диагональная матрица, то для выполнения условия автономности произведение (W_о^u·W_к^u·W_р^u) также должно быть диагональной матрицей:

R=W_о^u·W_к^u·W_р^u, (2.9)

где R=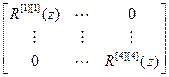– диагональная матрица, 4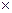4, diag[R]=diag[W_о^u·W_к^u·W_р^u].

Поскольку W_р^u – диагональная матрица, то из (2.9) следует, что матрица R будет диагональной в том случае, если произведение (W_о^u·W_к^u) также является диагональной матрицей. Приравнивая недиагональные элементы матрицы (W_о^u·W_к^u) к нулю, запишем полученную систему линейных уравнений:

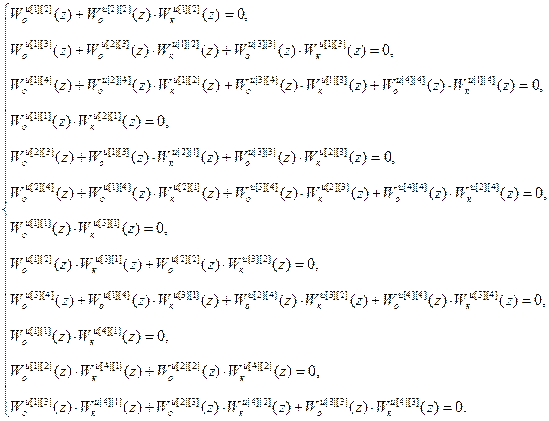(2.10)

В результате решения системы (2.10) получены передаточные функции компенсаторов перекрестных связей:

; ; ;

;

;

;

.

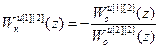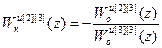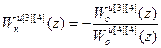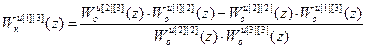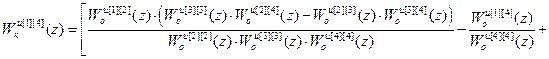
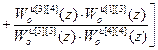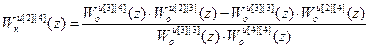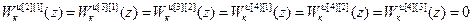Отсюда матрица дискретных передаточных функций компенсаторов перекрестных связей примет следующий вид:

.

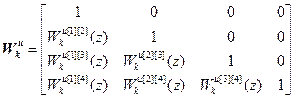В результате выполнения первого этапа расчета управляющей части системы с учетом несимметричной топологии связей ОУ получены формулы для расчета дискретных передаточных функции компенсаторов перекрестных связей из условия автономности.

Дата добавления: 2014-03-11; просмотров: 492; Нарушение авторских прав

Мы поможем в написании ваших работ!