Расчет параметров основных цифровых регуляторов

Для анализа входов и выходов связанной системы управления перейдем от векторно-матричной формы (2.8) к скалярной:

. (2.11)

Анализ выражения (2.11) показывает, что 4-х мерную ЦСУ (рис. 2.2) при выполнении условия автономности можно представить эквивалентной схемой в виде совокупности четырех одномерных (одноконтурных) систем (рис. 2.4), каждая из которых включает соответствующий основной регулятор связанной системы (2.12) и эквивалентный объект с передаточной функцией (2.13):

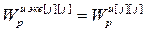, (2.12)

, j=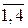. (2.13)

Рис. 2.4. Эквивалентная структурная схема АвЦСУ.

На основе полученных выражений (2.12)-(2.13) можно сделать следующие выводы:

1. Передаточные функции эквивалентных объектов многосвязного несимметричного ОУ (см. рис. 2.4) совпадают с передаточными функциями основных каналов (см. рис. 2.3).

2. Структура передаточных функций эквивалентных объектов не зависит от передаточных функций перекрестных каналов и передаточных функций компенсаторов перекрестных связей. Это в свою очередь приводит к значительному ускорению процедуры оптимизации параметров основных цифровых регуляторов, при этом улучшается сходимость оптимизируемого критерия к оптимуму.

Анализ (2.11) показывает, что в АвЦСУ каждая из управляемых величин 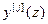является функцией только соответствующего задающего воздействия и алгоритма управления 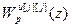. Следовательно, расчет параметров основных цифровых регуляторов управляющей части системы сводится к задаче скалярной оптимизации в одноконтурной системе на основе разностных уравнений соответствующих эквивалентных объектов.

Оптимизация параметров основных цифровых регуляторов может проводиться с использованием различных критериев. Наиболее часто для этих целей применяется квадратичная интегральная оценка, аналогом которой при построении дискретных систем управления является сумма квадратов ошибок управления:

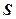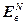=, (2.14)

где 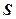=[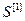,…,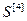]^Т – вектор критериев каждой управляемой величины;

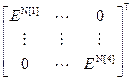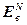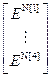=, =– блочная матрица и блочный вектор;

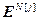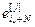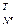=[,…,]– вектор дискретных значений ошибок для j-ой управляемой величины; N^в=N+1 – объем выборки дискретных значений ошибок на период времени переходного процесса j-ой управляемой величины; – индексы такта квантования.

Условие экстремума примет вид:

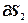=2·=0, (2.15)

где 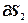=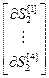– блочный вектор; 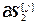=[,…,,,…,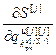]^Т – вектор частных производных j-го критерия по всем настройкам j-го регулятора, 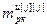; =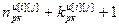– число переменных состояния разностного уравнения, описывающего динамические свойства регулятора, j=;

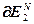=, =– блочная матрица и блочный вектор;

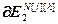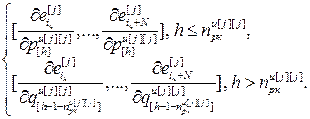=– матрица-строка значений частной производной j-ой ошибки управления по h-ой настройке j-го регулятора, N^в; j=, h=.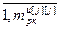

Поведение многомерной системы с учетом выражений (2.11)-(2.13) описывается следующей системой векторно-матричных уравнений:

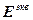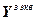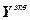=-, (2.16)

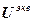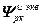
=, (2.17)

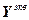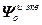
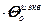=, (2.18)

где 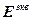– вектор ошибки управления; 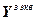– вектор заданий; 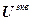=[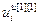,…,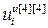]^Т – вектор выходов регуляторов;

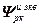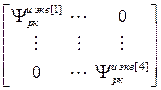=– блочная матрица; 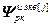– матрица-строка переменных состояния j-го регулятора; ;

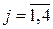– вектор настроечных параметров регуляторов; 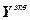– вектор управляемых величин;

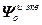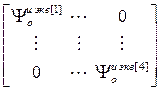=– блочная матрица;

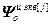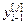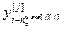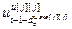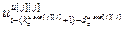=[,…,,,…,] – матрица-строка переменных состояния j-го эквивалентного ОУ, ; ;

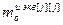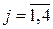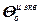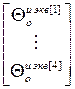=– блочный вектор; 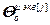=[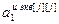,…,,,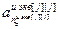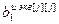…,]^T – вектор параметров j-го эквивалентного ОУ, 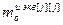; 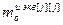=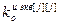++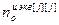1 – число переменных состояния эквивалентного ОУ; 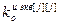, 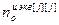– порядки числителя и знаменателя дискретной передаточной функции эквивалентного ОУ; – число тактов запаздывания эквивалентного ОУ; .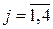

Расчет численных значений частных производных в векторно-матричной форме с учетом выражений (2.11)-(2.13):

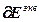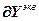=-, (2.19)

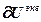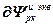
=+, (2.20)

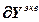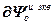
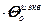=, (2.21)

где 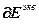– вектор частных производных всех ошибок управления по всем настройкам соответствующих регуляторов;

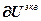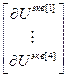=– блочный вектор; 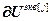=[,…,,,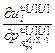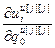…,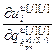]^Т – вектор частных производных выхода j-го регулятора по всем его настройкам, ; ;

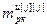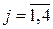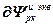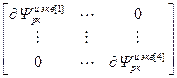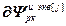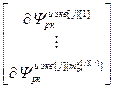=, =– блочная матрица и блочный вектор;

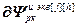=– матрица-строка частных производных переменных состояния j-го регулятора по его h-ой настройке, ; ;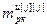

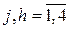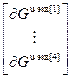=– блочный вектор; 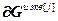=(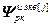)^T – вектор переменных состояния j-го регулятора, используемых для расчета значений частных производных его выхода; ;

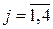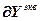– вектор частных производных выходов управляемых величин по всем настройкам соответствующих регуляторов;

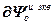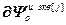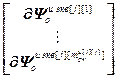=, =– блочная матрица и блочный вектор;

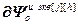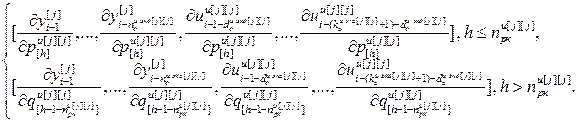=– матрица-строка частных производных переменных состояния j-го эквивалентного объекта управления по h-ой настройке j-го регулятора, ; .

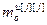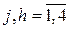После проведения первого этапа оптимизации, на котором в результате решения систем уравнений (2.16) – (2.21) вычисляются в начале векторы 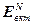и 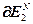, а затем значения вектора 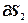(2.15), выполняется второй этап, на котором производится шаг по каждой настройке в направлении убывания критерия:

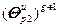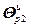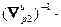
=(–)^g, (2.22)

где g – номер итерации приближения к оптимуму; 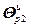=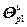– вектор настроечных параметров алгоритмов управления регуляторов;

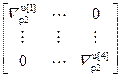=– блочная матрица; 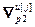=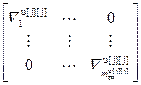– матрица нормы градиента j-го критерия, ;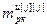

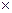
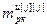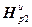– матрица коэффициентов шага; j=.

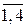Для вычисления коэффициента шага используются следующие выражения, записанные в матричной форме:

dia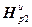g[()^g]=(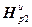)^g-1·(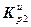)^g, (2.23)

где 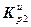– вектор переменных коэффициентов.

Значение j-го элемента вектора 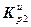определяется выражением:

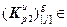
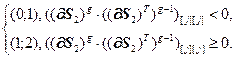(2.24)

Норма градиента вычисляется с помощью зависимости:

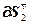=()^Т∙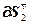, (2.25)

где 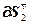=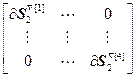, 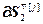=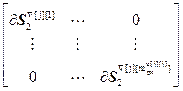– блочные матрицы;

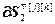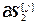=– вектор частных производных j-го критерия по всем настройкам j-го регулятора; j=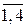, h=.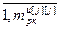

Момент окончания поиска оптимума определяется выполнением предварительно заданных условий:

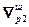<, (2.26)

или

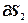<, (2.27)

где 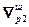=[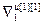,…,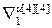]^Т – вектор норм градиента всех критериев; =[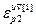,…,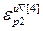]^Т – вектор заданной точности расчета оптимальных значений настроек всех регуляторов при использовании условия (2.26);

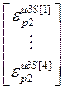=– блочный вектор; 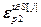=[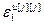,…,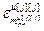]^Т – вектор заданной точности расчета оптимальных значений настроек j-го регулятора при использовании условия (2.27), 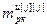; j=.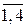

Для выполнения расчета выражений (2.16) – (2.18) и (2.19) – (2.21) необходимо предварительно задаться начальными условиями:

, , , ,

, ,

,

,

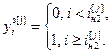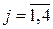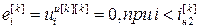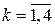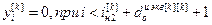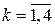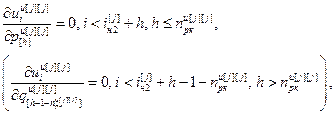
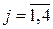
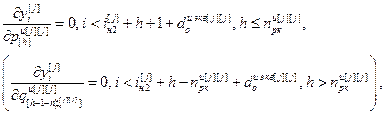
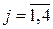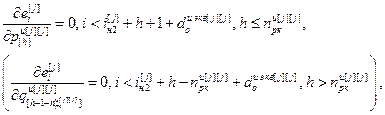
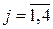где i_н2^[j]=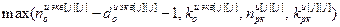– значение номера такта, с которого начинается расчет переходного процесса .

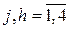Таким образом, предложен алгоритм оптимизации параметров основных цифровых регуляторов в составе АвЦСУ. Преимуществом данного алгоритма является возможность использования значительно менее мощных средств ЦВТ с относительно небольшими объемами оперативной памяти, при этом реализация рассмотренного алгоритма может проводиться как с использованием широко известных языков программирования (C++, Pascal, Fortran), так и с помощью вычислительных математических пакетов (MathCAD, Matlab, Maple).

Дата добавления: 2014-03-11; просмотров: 510; Нарушение авторских прав

Мы поможем в написании ваших работ!