ЗНАЧЕНИЕ ЛОГИКИ В ПРОЦЕССЕ ПОЗНАНИЯ

Расчет инвариантных компенсаторов возмущений

Следующим этапом расчета управляющей части системы является расчет компенсаторов возмущений из условия инвариантности.

Из соотношения (2.7) получим выражение для расчета передаточных функций компенсаторов возмущений, удовлетворяющих условию инвариантности:

W_к^f=(W_к^u)^-1·(W_о^u)^-1·(-W_o^f). (2.28)

Выражая из (2.9) (W_о^u)^-1:

(W_о^u)^-1=W_к^u·W_р^u·R^-1, (2.29)

можно записать эквивалентную формулу расчета передаточных функций компенсаторов возмущений:

W_к^f=(W_к^u)^-1·W_к^u·W_р^u·R^-1·(-W_o^f),

W_к^f=W_р^u·R^-1·(-W_o^f). (2.30)

Поскольку при выполнении условия автономности R является диагональной матрицей, то из (2.30) получим формулу расчета передаточных функций инвариантных компенсаторов возмущений:

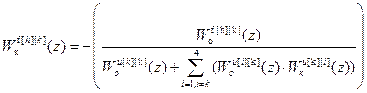. (2.31)

Используя (2.31) получим передаточные функции компенсаторов возмущений.

;

;

;

;

;

;

;

;

;

;

;

.

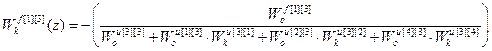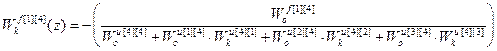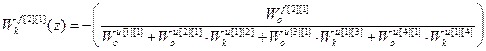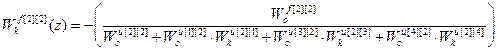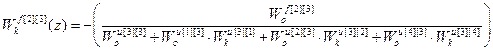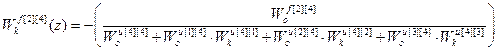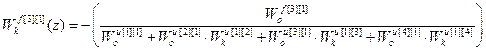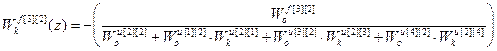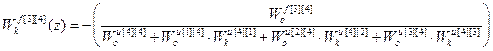С учетом структуры матрицы дискретных передаточных функций объекта по каналам управления W_о^u и возмущения W_о^f, а так же матрицы дискретных передаточных функций компенсаторов перекрестных связей W_к^u получаем:

; ;;

; ; ;

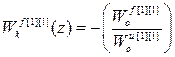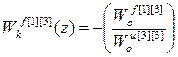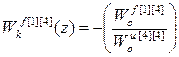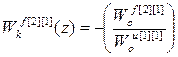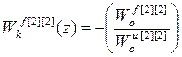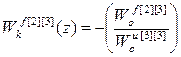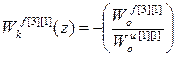; ; ; (2.32)

; ; .

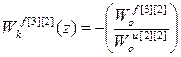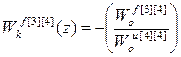Анализ передаточных функций компенсаторов возмущений (2.32) позволяет сделать следующие выводы:

1. Структура передаточных функций компенсаторов возмущений многосвязного несимметричного объекта имеет достаточно простую структуру.

2. Динамика компенсаторов возмущений не зависит от передаточных функций перекрестных каналов многосвязного объекта и компенсаторов перекрестных связей.

Таким образом, для несимметричного многосвязного объекта – процесса синтеза аммиака – разработана структура цифровой связно-комбинированной системы управления, выведены формулы для расчета компенсаторов перекрестных связей из условия автономности и компенсаторов возмущений из условия инвариантности, получены передаточные функции эквивалентных объектов и предложен алгоритм оптимизации параметров основных цифровых регуляторов по среднеквадратичному критерию качества. Кроме того, поскольку передаточные функций компенсаторов возмущений не зависят от динамики передаточных функций компенсаторов перекрестных связей и передаточных функций перекрестных каналов, то для несимметричных ОУ 2 и 3 этапы расчета управляющей части системы (п. 2.2.1) алгоритма можно выполнять независимо друг от друга, а при достаточных возможностях средств цифровой вычислительной техники – одновременно.

Логика – одна из самых старых наук. Ее богатая событиями история началась еще в Древней Греции и насчитывает две с половиной тысячи лет. В конце XIX – начале XX века в логике произошла научная революция, в результате которой в корне изменились стиль рассуждений, методы, и наука как бы обрела второе дыхание. Теперь логика – одна из наиболее динамичных наук, образец строгости и точности даже для математических теорий.

Законы логики лежат в основе нашего мышления. Интуитивно они известны каждому. Всякое движение мысли, постигающей истину и добро, опирается на эти законы и без них невозможно. В этом смысле логика общеизвестна.

Один из героев комедии Мольера только случайно обнаружил, что он всю жизнь говорил прозой. Так и с усвоенной стихийно логикой. Можно постоянно применять ее законы и вместе с тем не иметь ясного представления ни об одном из них.

Подобно тому, как умение говорить существовало еще задолго до грамматики, так и искусство правильно мыслить существовало до возникновения науки логики.

Лет триста назад авторы книг по логике считали своим долгом предостеречь читателя от торопливости при чтении: «В водах логики не следует плыть с полными парусами». С тех пор логика сделала гигантский шаг вперед. Ее содержание расширилось и углубилось. И старый этот совет кажется теперь особенно полезным.

Правильное рассуждение

Слово «логика» употребляется довольно часто, но в разных значениях.

Нередко говорят о логике событий, логике характера и т.п. В этих случаях имеется в виду определенная последовательность и взаимозависимость событий или поступков, наличие в них некоторой общей линии.

Слово «логика» употребляется также в связи с процессами мышления. Так, мы говорим о логичном и нелогичном мышлении.

В третьем смысле «логика» является именем особой науки о мышлении, называемой также формальной логикой.

Формальная логика – наука о законах и операциях правильного мышления.

Основной задачей логики является отделение правильных способов рассуждения (выводов, умозаключений) от неправильных.

Правильные рассуждения называются также обоснованными, последовательными или логичными.

Рассуждение представляет собой определенную, внутренне обусловленную связь утверждений.

От нашей воли зависит, на чем остановить свою мысль. В любое время мы можем прервать начатое рассуждение и перейти к другой теме. Но если мы решим провести его до конца, то сразу же попадем в сети необходимости, стоящей выше нашей воли и желаний. Согласившись с одними утверждениями, мы вынуждены принять и те, что из них следуют, независимо от того, нравятся они нам или нет, способствуют нашим целям или, напротив, препятствуют им. Допустив одно, мы тем самым автоматически лишаем себя возможности утверждать другое, несовместимое с уже допущенным.

Правильным является следующий вывод, использовавшийся в качестве стандартного примера еще в Древней Греции:

Все люди смертны; Сократ – человек; следовательно, Сократ смертен.

Первые два высказывания – это посылки рассуждения, третье – его заключение.

Схема данного рассуждения проста: если есть первое, то есть и второе. Принципиально важным является то, что, о чем бы мы ни рассуждали по такой схеме, рассуждение останется правильным. Чтобы убедиться в этом, достаточно подставить в схему вместо слов «первое» и «второе» два утверждения с любым конкретным содержанием.

Рассмотрим схему следующего рассуждения: если есть первое, то есть и второе; имеет место первое; значит, есть и второе.

Пример. Если идет дождь, земля мокрая; идет дождь; следовательно, земля мокрая.

Изменим несколько данную схему и будем рассуждать так: если есть первое, то имеется второе; имеет место второе; значит, есть и первое.

Пример. Если идет дождь, земля мокрая; земля мокрая; следовательно, идет дождь.

Этот вывод, очевидно, неправилен. Верно, что всякий раз, когда идет дождь, земля мокрая. Но из этого условного утверждения и того факта, что земля мокрая, вовсе не вытекает, что идет дождь. Земля может оказаться мокрой и без дождя, ее можно намочить, скажем, из шланга, она может быть мокрой после таяния снега и т.д.

Отличительная особенность правильного рассуждения заключается в том, что от истинных посылок оно всегда ведет к истинному заключению.

Этим объясняется тот огромный интерес, который логика проявляет к правильным рассуждениям. Они позволяют из уже имеющегося знания получать новое знание, и притом с помощью «чистого» рассуждения, без всякого обращения к опыту, интуиции и т.п.

Если посылки, или хотя бы одна из них, являются ложными, правильное рассуждение может давать в итоге как истину, так и ложь. Неправильные рассуждения могут от истинных посылок вести как к истинным, так и к ложным заключениям. Никакой определенности здесь нет. С логической необходимостью заключение вытекает только в случае правильных, обоснованных рассуждений.

Логическая форма

Основной принцип формальной логики. Правильность рассуждения зависит только от его логической формы.

Форма рассуждения – способ связи входящих в это рассуждение содержательных частей.

Каждое наше рассуждение, каждая мысль, выраженная в языке, имеет не только определенное содержание, но и определенную форму. Предполагается также, что содержание и форма отличаются друг от друга и могут быть разделены. Содержание мысли не оказывает никакого влияния на правильность рассуждений, и поэтому от него следует отвлечься. Для оценки правильности мысли существенной является лишь ее форма.

Примеры. Сравним два высказывания: «Все вороны – птицы», «Все шахматисты – гроссмейстеры». По содержанию они совершенно различны, к тому же первое является истинным, а второе ложным. И, тем не менее, сходство их несомненно. Это сходство ‒ в их строении, форме. Чтобы выявить такое сходство, нужно отвлечься от содержания высказываний.

Заменим все содержательные компоненты высказываний латинскими буквами, скажем S и Р, не несущими никакого содержания. В итоге получим в обоих случаях одно и то же:

«Все S есть Р».

Это и есть форма рассматриваемых высказываний. Она получена в результате отвлечения от конкретного их содержания. Но и сама эта форма имеет все-таки некоторое содержание. Из нее мы узнаем, что у всякого предмета, обозначаемого буквой S, есть признак, обозначаемый буквой Р.

Этот простой пример хорошо показывает одну из особенностей подхода формальной логики к анализу рассуждений – его высокую абстрактность.

Пример. Рассмотрим далее два более сложных высказывания: «Если число делится на 2, то оно четное», «Если сейчас ночь, то сейчас темно». Для выявления логической формы этих высказываний подставим вместо их содержательных компонентов слова «первое» и «второе», не несущие конкретного содержания. В результате получим, что оба эти высказывания имеют одну и ту же логическую форму: «Если первое, то второе». Если вместо последних слов использовать буквенные переменные, скажем, А и В, получим: «Если А, то В». Это и есть логическая форма данных сложных высказываний.

Для выявления формы надо отвлечься от содержания мысли, заменить содержательные ее части пробелами или буквами. Останется только связь этих частей. В обычном языке она выражается словами: «все ... есть ...», «некоторые ... есть...», «если..., то...», «... и ...», «... или ...», «неверно, что ...» и т.п.

Дедукция и индукция

Умозаключение – это логическая операция, в результате которой из одного или нескольких принятых утверждений (посылок) получается новое утверждение – заключение (следствие).

В зависимости от того, существует ли между посылками и заключением связь логического следования, можно выделить два вида умозаключений.

Дедуктивное умозаключение – такое умозаключение, в котором связь посылок и заключения опирается на логический закон, в силу чего заключение с логической необходимостью вытекает из принятых посылок.

Отличительная особенность такого умозаключения в том, что оно от истинных посылок всегда ведет к истинному заключению.

Пример. К дедуктивным относится, например, такое умозаключение:

Если данное число делится на 6, то оно делится на 3.

Данное число делится на 6.

Данное число делится на 3.

Черта, отделяющая посылки от заключения, заменяет слово «следовательно».

Индуктивное умозаключение – такое умозаключение, в котором связь посылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера.

В таком умозаключении заключение не следует логически из посылок и может содержать информацию, отсутствующую в них. Достоверность посылок не означает поэтому достоверности выведенного из них индуктивно утверждения.

Индукция дает только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.

Пример.

Аргентина является республикой.

Бразилия – республика.

Венесуэла – республика.

Эквадор – республика.

Аргентина, Бразилия, Венесуэла, Эквадор – латиноамериканские государства.

Все латиноамериканские государства являются республиками.

Пример.

Италия – республика.

Португалия – республика.

Финляндия – республика.

Франция – республика.

Италия, Португалия, Финляндия, Франция – западноевропейские страны.

Все западноевропейские страны являются республиками.

Индукция не дает полной гарантии получения новой истины из уже имеющихся. Максимум, о котором можно говорить, ‒ это определенная степень вероятности выводимого утверждения.

Так, посылки и первого, и второго индуктивного умозаключения истинны, но заключение первого из них истинно, а второго – ложно. Действительно, все латиноамериканские государства – республики. Но среди западноевропейских стран имеются не только республики, но и монархии, например, Англия, Бельгия и Испания.

Особенно характерными дедукциями являются логические переходы от общего знания к частному.

Рассуждения, ведущие от знания о части предметов к общему знанию обо всех предметах определенного класса, – это типичные индукции, поскольку всегда остается вероятность того, что обобщение окажется поспешным и необоснованным.

Нельзя вместе с тем отождествлять дедукцию с переходом от общего к частному, а индукцию – с переходом от частного к общему.

Дедукция – это логический переход от одной истины к другой, индукция – переход от достоверного знания к вероятному.

Дедукция – собственно логический способ обоснования утверждений, использующий чистое рассуждение и не требующий обращения к наблюдению, интуиции и т.д.

К индуктивным умозаключениям относятся не только обобщения, но и аналогии, заключения о причинах явлений и др.

Не следует недооценивать индукцию. Почти все общие положения, включая, конечно, и научные законы, являются результатом индуктивного обобщения. В этом смысле индукция – основа нашего знания. Сама по себе она не гарантирует его истинности и обоснованности. Но она порождает предположения, связывает их с опытом и тем самым сообщает им определенное правдоподобие, более или менее высокую степень вероятности. Опыт – источник и фундамент человеческого знания. Индукция, отправляющаяся от того, что постигается в опыте, является необходимым средством его обобщения и систематизации.

В обычных рассуждениях дедукция только в редких случаях предстает в полной и развернутой форме. Чаще всего мы указываем не все используемые посылки, а лишь некоторые из них. Общие утверждения, о которых можно предполагать, что они хорошо известны, как правило, опускаются. Не всегда явно формулируются и заключения, вытекающие из принятых посылок. Сама логическая связь, существующая между исходными и выводимыми утверждениями, лишь иногда отмечается словами, подобными «следовательно» и «значит». Нередко дедукция является настолько сокращенной, что о ней можно только догадываться.

Проводить дедуктивное рассуждение, ничего не опуская и не сокращая, обременительно. Человек, указывающий все предпосылки своих заключений, создает впечатление какого-то педанта. И вместе с тем всякий раз, когда возникает сомнение в обоснованности сделанного вывода, следует возвращаться к самому началу рассуждения и воспроизводить его в возможно более полной форме. Без этого трудно или даже просто невозможно обнаружить допущенную ошибку.

Понятие «правильное рассуждение (умозаключение)» относится только к дедуктивному умозаключению. Лишь оно может быть правильным или неправильным. В индуктивном умозаключении вывод не связан логически с принятыми посылками. Поскольку «правильность» – это характеристика логической связи между посылками и заключением, а индуктивным умозаключением данная связь не предполагается, такое умозаключение не может быть ни правильным, ни неправильным.

Интуитивная логика

Под интуитивной логикой обычно понимают интуитивные представления о правильности рассуждений, сложившиеся стихийно в процессе повседневной практики мышления. Интуитивная логика, как правило, успешно справляется со своими задачами в повседневной жизни, но совершенно недостаточна для критики неправильных рассуждений.

Пример. Правильно ли рассуждает человек, когда говорит: «Если бы барий был металлом, он проводил бы электрический ток; барий проводит электрический ток; следовательно, он металл?». Чаще всего на основе логической интуиции отвечают: правильно, барий металл, и он проводит ток. Этот ответ, однако, неверен. Хотя все три утверждения, входящие в рассуждение, верны, между ними нет логической связи. Рассуждение построено по неправильной схеме: «Если есть первое, то есть второе; второе есть; значит, есть и первое». Такая схема от истинных исходных положений может вести не только к истинному, но и к ложному заключению, она не гарантирует получения новых истин из имеющихся.

Пример. В рассуждении: «Если у человека повышенная температура, он болен; человек болен; следовательно, у него повышенная температура» обе посылки могут быть истинными, а заключение ложным: многие болезни протекают без повышения температуры.

Логическая правильность зависит только от способа связи утверждений. Она не зависит от того, истинны используемые в рассуждении посылки или нет.

Простые примеры показывают, что логика, усвоенная стихийно, даже в обычных ситуациях может оказаться ненадежной.

Навык правильного мышления не предполагает каких-либо теоретических знаний, умения объяснить, почему что-то делается именно так, а не иначе. К тому же сама интуитивная логика, как правило, беззащитна перед лицом критики.

Традиционная и современная логика

В истории логики отчетливо выделяются два основных этапа. Первый – от древнегреческой логики до возникновения во второй половине XIX века современной логики. Второй – с того времени до наших дней.

Первый этап обычно называется традиционной логикой. Формальная логика развивалась очень медленно. Обсуждавшиеся в ней проблемы мало чем отличались от проблем, поставленных еще Аристотелем. Это дало повод Канту прийти к выводу, что формальная логика является завершенной наукой, не продвинувшейся со времени Аристотеля ни на один шаг.

Кант не заметил, что еще с XVII века стали назревать предпосылки для научной революции в логике. Именно в это время получила ясное выражение идея представить доказательство как вычисление, подобное вычислению в математике.

Эта идея связана, главным образом, с именем Лейбница. По Лейбницу, вычисление суммы или разности чисел осуществляется на основе простых правил, принимающих во внимание только форму чисел, а не их смысл. Результат вычисления однозначно предопределяется этими, не допускающими разночтения правилами, и его нельзя оспорить. Лейбниц мечтал о времени, когда умозаключение будет преобразовано в вычисление. Когда это случится, споры между философами станут невозможны. Вместо спора они возьмут в руки перья и скажут: «Будем вычислять». Идеи Лейбница не оказали заметного влияния на его современников. Энергичное развитие логики началось лишь в XIX веке.

Немецкий математик и логик Готлоб Фреге (1848 ‒ 1925) в своих работах стал применять формальную логику для исследования оснований математики. Фреге был убежден, что «арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никакого обоснования». Пытаясь свести математику к логике, он реконструировал саму логику. Логическая теория Фреге – провозвестник всех нынешних теорий правильного рассуждения.

Идея сведения всей чистой математики к логике была подхвачена английским логиком и философом Бертраном Расселом (1872 ‒ 1970). Но последующее развитие логики показало неосуществимость этой попытки. Она привела, однако, к широкому проникновению плодотворных методов математики в логику.

Современную логику нередко называют математической, подчеркивая тем самым своеобразие новых ее методов в сравнении с использовавшимися ранее в традиционной логике. Одна из характерных особенностей этих методов – широкое использование разнообразных символов вместо слов и выражений обычного языка. Символы применял в ряде случаев еще Аристотель, а затем и все последующие логики. Однако со второй половины XIX века в использовании символики был сделан качественно новый шаг. В логике стали использоваться специально построенные языки, содержащие только специальные символы и не включающие ни одного слова обычного разговорного языка.

Широкое использование символических средств послужило основанием того, что, новую логику стали называть символической. Названия «математическая логика» и «символическая логика» обозначают одно и то же – современную формальную логику. Она занимается тем же, чем всегда занималась логика, – исследованием правильных способов рассуждения.

Современная логика и другие науки

В течение многих веков логика считалась, подобно психологии, одной из «философских наук». И только во второй половине XIX века формальная – к этому времени уже математическая – логика «отпочковалась» от философии. Примерно в это же время от философии отделилась и стала самостоятельной научной дисциплиной психология. Но если отделение психологии было связано, прежде всего, с проникновением в нее опыта и эксперимента и сближением ее с другими эмпирическими науками, то в отделении логики решающую роль сыграло проникновение в нее математических методов и сближение с математикой.

Согласно Фреге, Расселу и их последователям, математика и логика – это всего лишь две ступени в развитии той же самой науки. Математика может быть полностью сведена к логике, и такое чисто логическое обоснование математики позволит установить ее истинную и наиболее глубокую природу. Этот подход к обоснованию математики получил название логицизма.

Сторонники логицизма добились определенных успехов в прояснении основ математики. В частности, было показано, что математический словарь сводится к неожиданно краткому перечню основных понятий, которые принадлежат словарю чистой логики. Вся существующая математика была сведена к сравнительно простой и унифицированной системе исходных, принимаемых без доказательства положений, или аксиом, и правил вывода из них следствий, или теорем. В целом логицизм оказался утопической концепцией.

Математика несводима к логике, поскольку для построения математики необходимы аксиомы, устанавливающие существование в реальности определенных объектов. Но такие аксиомы имеют уже внелогическую природу.

Другой формой объединения математики и логики в одну науку было объявление современной логики одним из разделов современной математики.

Тенденция включать математическую логику в число математических дисциплин и видеть в ней только теорию математического доказательства является ошибочной. На самом деле задачи логики гораздо шире. Она исследует основы всякого правильного рассуждения, а не только строгого математического доказательства, и ее интересует связь между посылками и следствиями в любых областях познания.

Дата добавления: 2014-03-11; просмотров: 614; Нарушение авторских прав

Мы поможем в написании ваших работ!