Аналитические модели СМО

Как отмечено выше, аналитические модели СМО удается получить при довольно серьезных допущениях. К числу типичных допущений относятся следующие.

Во–первых, как правило, считают, что в СМО используются бесприоритетные дисциплины обслуживания типа FIFO.

Во–вторых, времена обслуживания заявок в устройствах выбираются в соответствии с экспоненциальным законом распределения.

В–третьих, в аналитических моделях СМО входные потоки заявок

аппроксимируются простейшими потоками, т.е. потоками, обладающими свойствами стационарности, ординарности (невозможности одновременного поступления двух заявок на вход СМО), отсутствия последействия.

В большинстве случаев модели СМО отображают процессы с конечным множеством состояний и с отсутствием последействия. Такие процессы называют конечными марковскими цепями.

Марковские цепи характеризуются множеством состояний S, матрицей вероятностей переходов из одного состояния в другое и начальными условиями (начальным состоянием). Удобно представлять марковскую цепь в виде графа, в котором вершины соответствуют состояниям цепи, дуги – переходам, веса дуг – вероятностям переходов (если время дискретно) или интенсивностям переходов ( если время непрерывно).

Отметим, что интенсивностью перехода называют величину Vij =lim Pij(t1) / t1 при t1→0, где Pij(t1) – вероятность перехода из состояния Si в состояние Sj за время t1. Обычно принимается условие

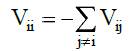
что означает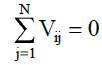

где N – число состояний. На рис. 15.6приведен пример марковской цепи

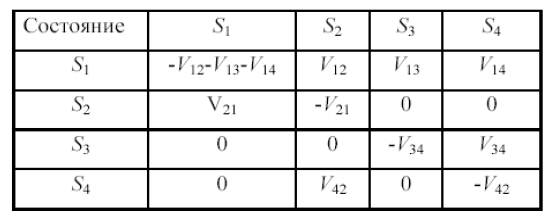
в виде графа с состояниями S1,...,S4, а в таблице 15.1 представлена матри-

ца интенсивностей переходов для этого примера.

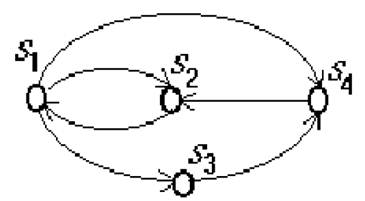
Рис.15.6. Пример марковской цепи

Большинство выходных параметров СМО можно определить, используя информацию о поведении СМО, т.е. информацию о состояниях СМО в установившихся (стационарных) режимах и об их изменениях в переходных процессах. Эта информация имеет вероятностную природу, что обусловливает описание поведения СМО в терминах вероятностей нахождения системы в различных состояниях. Основой такого описания, а следовательно, и многих аналитических моделей СМО являются уравнения Колмогорова, которые можно получить следующим образом.

Таблица 15.1 Матрица интенсивности переходов

Изменение вероятности Pi нахождения системы в состоянии Si за время t1 есть вероятность перехода системы в состояние Si из любых других состояний за вычетом вероятности перехода из состояния Si в другие состояния за время t1, т.е.

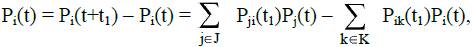
где Pi(t) и Pj(t) – вероятности нахождения системы в состояниях Si и Sj

соответственно в момент времени t, а Pji(t1) и Pik(t1) – вероятности изменения состояний в течение времени t1; произведение вида Pji(t1)Pj(t) есть безусловная вероятность перехода из Sj в Si, равная условной вероятности перехода, умноженной на вероятность условия; J и K – множества индексов инцидентных вершин по отношению к вершине Si по входящим и исходящим дугам на графе состояний соответственно

Дата добавления: 2014-02-26; просмотров: 710; Нарушение авторских прав

Мы поможем в написании ваших работ!