Аналитические методы вычисления интеграла

Определение: функция F(x) называется первообразной для функции f(x), если F’(x) = f(x) или dF(x) = f(x)dx.

Определение: неопределённым интегралом от функции f(x) (или от выражения f(x)dx) называется совокупность всех её первообразных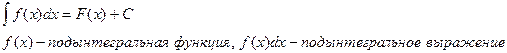

Процедура отыскания неопределённого интеграла называется интегрированием функции.

Определение: определённым интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при условии, что число элементарных отрезков n стремиться к бесконечности, а длина наибольшего из них стремиться к нулю .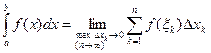

Теорема существования определенного интеграла: если функция f(x) непрерывна на отрезке [a,b], то предел интегральной суммы существует и не зависит от способа разбиения отрезка [a,b] на элементарные и от выбора точек ξ_к .

Вычисляют определённый интеграл по формуле Ньютона-Лейбница: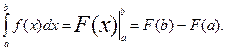

Вычисление интеграла аналитическими методами осуществляется в системе MATLAB с помощью функций 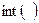, которые имеют вид:

,

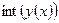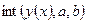
где: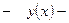подынтегральная функция; 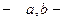пределы интегрирования.

Эти функции вычисляют:

- неопределенный интеграл;

- неопределенный интеграл с символьными переменными;

- определенный интеграл с символьными значениями пределов интегрирования;

- определенный интеграл от алгебраических функций;

- кратные интегралы;

- несобственные интегралы.

Технология вычисления интегралов состоит в следующем:

1. Определение символьных переменных с помощью функции .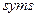

2. Ввод подынтегральной функции с присвоением ему имени: ;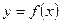

3. Ввод функции 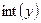, если вычисляется неопределенный интеграл, или функция 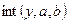, если вычисляется определенный интеграл в пределах .

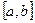4. Получение решения путем нажатия клавиши “Enter”.

Пример:

Необходимо вычислить следующий интеграл: .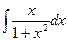

Решение:

>> syms x;

>> y=x/(1+x^2);

>> int(y)

ans = 1/2*log(1+x^2)

Пример:

Вычислить интеграл: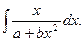

Здесь имеем случай, когда подынтегральная функция задана в аналитическом виде с символьными переменными.

Решение имеет вид:

>> syms x a b;

>> y=x/(a+b*x^2);

>> int(y)

ans = 1/2/b*log(a+b*x^2)

Пример:

Вычислить значение определенного интеграла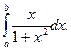

Здесь пределы интегрирования заданы в символьных переменных.

Решение:

>> syms x a b;

>> y=x/(1+x^2);

>> int(y,a,b)

ans = 1/2*log(1+b^2)-1/2*log(1+a^2)

Пример:

Вычислить определенный интеграл: .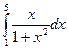

Решение:

>> syms x;

>> y=x/(1+x^2);

>> int(y,1,5)

ans = 1/2*log(13).

Для получения решения в естественной форме достаточно активизировать с помощью мыши строку ответа и нажать клавишу «Enter». Будет получен следующий ответ ans = 1.2825.

Пример: 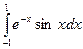вычислить интеграл, используя файл-функцию

function f=fint(x) % создаём файл-функцию и сохраняем её

f=exp(-x).*sin(x);

Используем файл-функцию для вычисления интеграла

syms x; I=int(fint(x),-1,1)

I =-1/2*exp(-1)*cos(1)-1/2*exp(-1)*sin(1)+1/2*exp(1)*cos(1)-1/2*exp(1)*sin(1)

>> vpa(I,4)

ans = -.6637

Дата добавления: 2014-03-11; просмотров: 750; Нарушение авторских прав

Мы поможем в написании ваших работ!