Вычисление несобственных интегралов

Если хотя бы одно из условий теоремы существования не выполняется, то речь идет о несобственном интеграле.

Несобственными интегралами называются:

1) интегралы с бесконечными пределами ;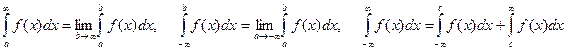

Предел сходится если интеграл существует и конечен.

2) интегралы от неограниченных функций, т.е. имеющих бесконечный разрыв в точке с на интервале [a,b]

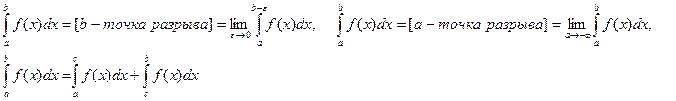
Предел сходится если интеграл существует и конечен.

Вычисления интегралов с бесконечными пределами с помощью функции 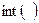имеют особенности, которые увидим при решении примеров.

Пример:

Необходимо вычислить следующий несобственный интеграл: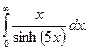

Решение:

>> syms x;

>> y=x/sinh(5*x);

>> int(y,0,inf)

ans = 1/100*pi^2.

Ответ: интеграл сходится

А теперь вычислим тот же интеграл, введя символьную переменную :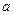

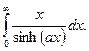
Повторим вычисление интеграла:

>> syms x a;

>> y=x/sinh(a*x);

>> int(y,0,inf)

ans = limit(1/2*(4*dilog(exp(-a*x))-dilog(exp(-2*a*x)))/a^2,x = inf).

Решение в явном виде не получено. Причина в том, что переменная 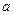не определена. Это может быть число положительное или отрицательное, действительное или комплексное. Пусть это число действительное и положительное. Тогда программа будет иметь вид:

>> syms x a;

>> y=x/sinh(abs(a)*x);

>> int(y,0,inf)

ans = 1/4*pi^2/abs(a)^2.

Функция 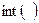позволяет вычислять достаточно сложные интегралы. Вот один из примеров.

Пример:

Требуется вычислить следующий несобственный интеграл:

.

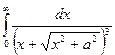Решение:

>> syms x a;

>> y=1/(x+sqrt(x^2+a^2))^3;

>> int(y,0,inf)

ans = 3/8/a^2.

Не нужно указывать программе на знак числа 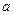и писать 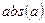, т.к. число 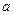возводится в квадрат и является положительным.

Дата добавления: 2014-03-11; просмотров: 569; Нарушение авторских прав

Мы поможем в написании ваших работ!