
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вычисление пределов от рациональной функции в конечной точке
Пример 2.1. Вычислить 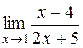 .
.
Так как знаменатель рациональной функции не обращается в 0 при 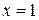 , то эта функция непрерывна в точке
, то эта функция непрерывна в точке 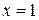 . Значит
. Значит
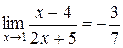
Пример 2.2. Вычислить 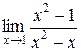 .
.
Числитель и знаменатель дроби равны нулю при 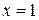 . В этом случае говорят, что имеет место неопределённость вида
. В этом случае говорят, что имеет место неопределённость вида 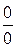 . В числителе разложим многочлен
. В числителе разложим многочлен 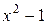 на множители по формуле
на множители по формуле 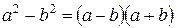 , в знаменателе вынесем за скобку общий множитель
, в знаменателе вынесем за скобку общий множитель 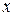 . Получим
. Получим
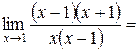
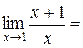
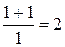 .
.
Пример 2.3. Вычислить 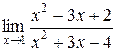 .
.
При подстановке 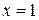 в выражение
в выражение 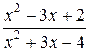 получаем неопределённость вида
получаем неопределённость вида 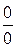 . Разложим многочлены
. Разложим многочлены 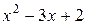 и
и 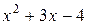 на множители. Напомним, как в общем случае можно найти корни квадратного трёхчлена
на множители. Напомним, как в общем случае можно найти корни квадратного трёхчлена 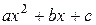 . Вычислим дискриминант
. Вычислим дискриминант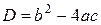 . Если
. Если 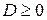 , то корни находим по формулам:
, то корни находим по формулам: 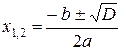 . Тогда
. Тогда  .
.
В нашем случае для трёхчлена 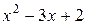
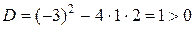 ,
, 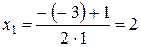 ,
, 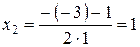 .
.
Поэтому 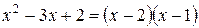 .
.
Таким же образом найдём корни квадратного трёхчлена 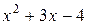 .
.
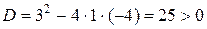 ,
, 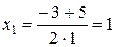 ,
, 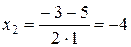 .
.
Тогда разложение на множители имеет вид 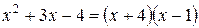 .
.
Итак, 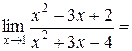
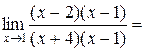
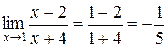 .
.
Следующие два примера решаются подобным образом.
Пример 2.4.
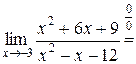
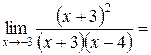
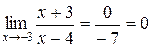 .
.
Пример 2.5.
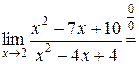

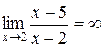 .
.
Пример 2.6. Вычислить 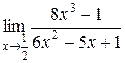 .
.
Многочлен 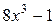 разложим на множители по формуле
разложим на множители по формуле
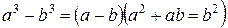 .
.
Для многочлена 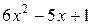 найдём корни
найдём корни
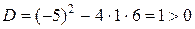 ,
, 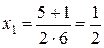 ,
, 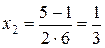 . Тогда
. Тогда
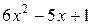 =
=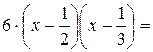
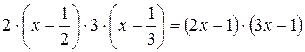 .
.
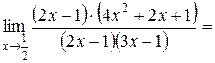
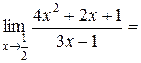
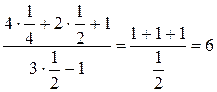 .
.
Пример 2.7. Вычислить 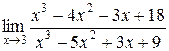 .
.
Имеет место неопределённость вида 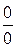 . Так как
. Так как 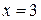 является корнем многочленов
является корнем многочленов 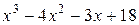 и
и 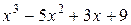 , то каждый из них делится без остатка на
, то каждый из них делится без остатка на 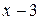 .
.
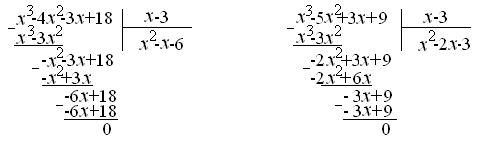
Получим 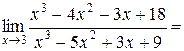
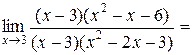
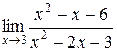 ;
;
Так как неопределённость 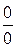 не исчезла, разложим на множители многочлены числителя и знаменателя.
не исчезла, разложим на множители многочлены числителя и знаменателя.
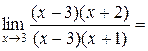
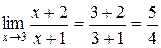 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление пределов на бесконечности | | | Вычисление пределов, содержащих иррациональность |
Дата добавления: 2014-02-28; просмотров: 625; Нарушение авторских прав

Мы поможем в написании ваших работ!