
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вычисление пределов на бесконечности
|
Читайте также: |
Пример 1.1 Найти 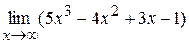 .
.
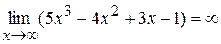 , так как
, так как 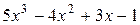 – многочлен
– многочлен
третьей степени является б.б. функцией при  .
.
Пример 1.2. Вычислить 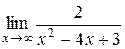 .
.
Имеем 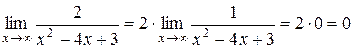 , так как
, так как
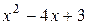 – б.б. функция при
– б.б. функция при  .
.
Пример 1.3. Вычислить 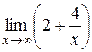 .
.
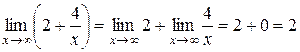 .
.
Пример 1.4. Вычислить  .
.
Так как 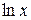 – непрерывная функция при
– непрерывная функция при 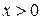 , то
, то
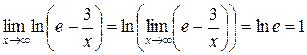 .
.
Пример 1.5. Вычислить 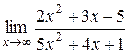 .
.
Числитель и знаменатель дроби представляют собой б. б. функции при  . В этом случае говорят, что имеет место неопределенность
. В этом случае говорят, что имеет место неопределенность 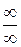 .
.
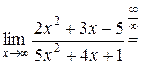
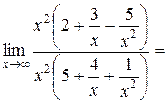
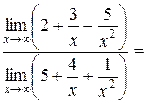
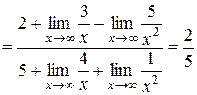 .
.
В дальнейшем не будем так подробно описывать применение свойств пределов.
Пример 1.6. Вычислить 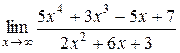 .
.
Имеем 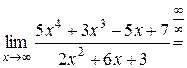
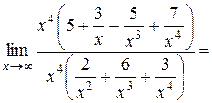
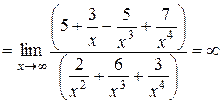 , так как числитель дроби при
, так как числитель дроби при  стремится к 5, а знаменатель является б.м. функцией.
стремится к 5, а знаменатель является б.м. функцией.
Пример 1.7. Вычислить 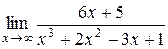 .
.
Разделим числитель и знаменатель дроби на 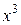 . Получим
. Получим
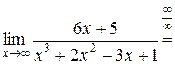
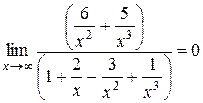 , так как числитель дроби при
, так как числитель дроби при  стремится к 0, а знаменатель – к 1.
стремится к 0, а знаменатель – к 1.
Проанализируем решение последних трёх примеров. Все они представляют собой предел отношения многочленов при  . В первом случае имело место равенство степеней многочленов числителя и знаменателя. Предел в этом случае равен отношению коэффициентов при старших степенях
. В первом случае имело место равенство степеней многочленов числителя и знаменателя. Предел в этом случае равен отношению коэффициентов при старших степенях 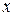 . Во втором примере в числителе – многочлен 4-ой степени, а в знаменателе – 2-ой степени. Предел отношения многочленов равен
. Во втором примере в числителе – многочлен 4-ой степени, а в знаменателе – 2-ой степени. Предел отношения многочленов равен 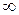 . Наконец, в 3-м примере в числителе стоит многочлен 1-ой степени, в знаменателе – 3-ей. Предел равен 0.
. Наконец, в 3-м примере в числителе стоит многочлен 1-ой степени, в знаменателе – 3-ей. Предел равен 0.
В общем случае имеет место правило: если
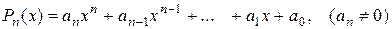 ,
, 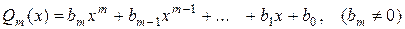 ,
,
то 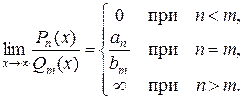 .
.
В дальнейшем можно пользоваться этим правилом при вычислении подобных примеров.
Пример 1.8.
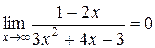 , так как
, так как 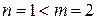 .
.
Пример 1.9.
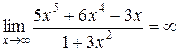 , так как
, так как 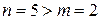 .
.
Пример 1.10.
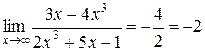 , так как
, так как 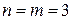 .
.
Пример 1.11.
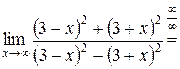
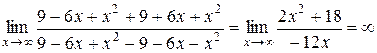 , так как
, так как 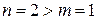 .
.
Пример 1.12.
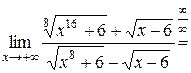
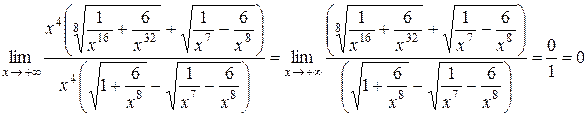 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Определения и понятия, которые известны из школьного курса | | | Вычисление пределов от рациональной функции в конечной точке |
Дата добавления: 2014-02-28; просмотров: 958; Нарушение авторских прав

Мы поможем в написании ваших работ!