Вычисление площадей

а) Если функция 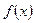непрерывна и неотрицательна на отрезке 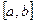, то площадь S криволинейной трапеции, ограниченной линиями 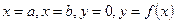, вычисляется по формуле

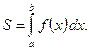
б) Есл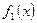и и 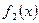непрерывные на отрезке 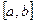функции, причем 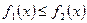на этом отрезке, то площадь фигуры, ограниченной линиями 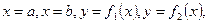вычисляется по формуле

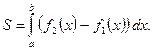
в) Если непрерывная кривая 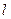задана параметрическими уравнениями 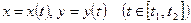, причем 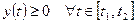, то площадь криволинейной трапеции, ограниченной этой кривой и прямыми 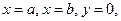выражается формулой

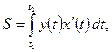
где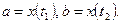

г) Площадь сектора AOB, ограниченного непрерывной кривой 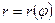(заданной в полярных координатах) и двумя лучами 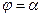и , равна

.

Дата добавления: 2014-02-28; просмотров: 591; Нарушение авторских прав

Мы поможем в написании ваших работ!