Вычисление координат вершин теодолитного хода

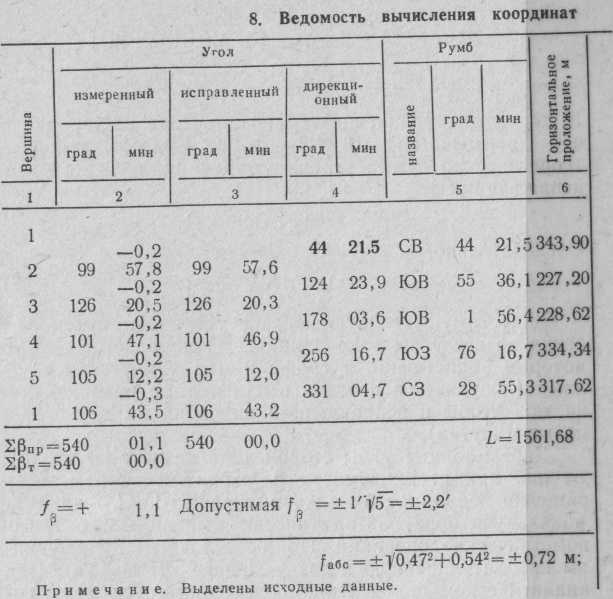
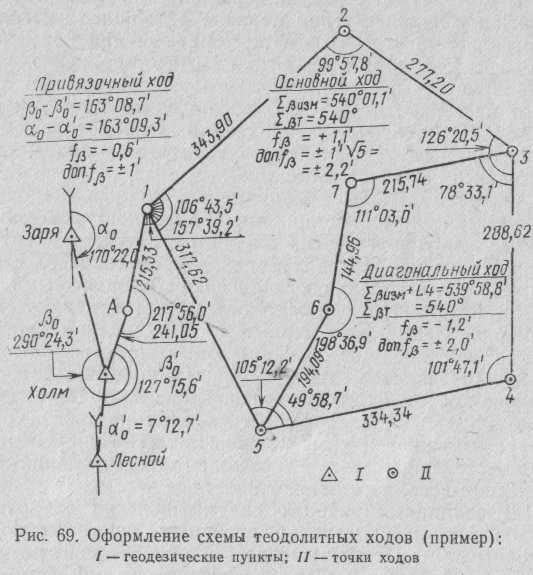Вначале проверяют полевой журнал: сличают записи, сделанные при измерении одной величины разными полуприемами и приемами; повторяют вычисления углов, длин сторон и приведение их к горизонту; оценивают, не выходят ли за пределы допусков погрешностиизмерений. На последней странице журнала отмечают, кем и когда он проведен. По проверенным данным составляют схему ходов (рис. 69). На схему наносят исходные и определяемые пункты, записывают результаты угловых и линейных измерений, а также контрольных вычислений. Дальнейшие вычисления записывают в ведомости (табл. 8); порядок вычислений соответствует номерам ее граф. После заполнения граф 1 и 2 находят угловую невязку. В замкнутом теодолитном ходе ее вычисляют так же, как и в буссолыюм (см. § 25).

Формулу вычисления угловой невязки разомкнутого хода (см. рис. 67, б) с правыми измеренными углами получим следующим путем. Имея исходные дирекцион-ные углы α_ав — α₀ и α_CD=α_n и вычислив последовательно дирекционные углы сторон хода по (5), получим

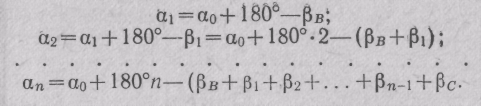
В последнем уравнении n— число углов хода, включая примычные; (β_Β + β₁ + β₂ + · · . + β_n-1 + β_C) = Σβ_T — теоретическая сумма углов, которую из того же уравнения запишем

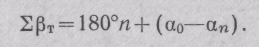
Следовательно,

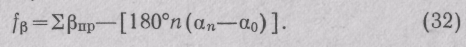
Допустимую угловую невязку устраняют путем введения во все углы хода одинаковых поправок ω_β = f_β/n, которые записывают в графе 2 над измеренными углами (допускается вводить в измеренные углы поправки так, чтобы в исправленном виде они выражались в целых минутах).

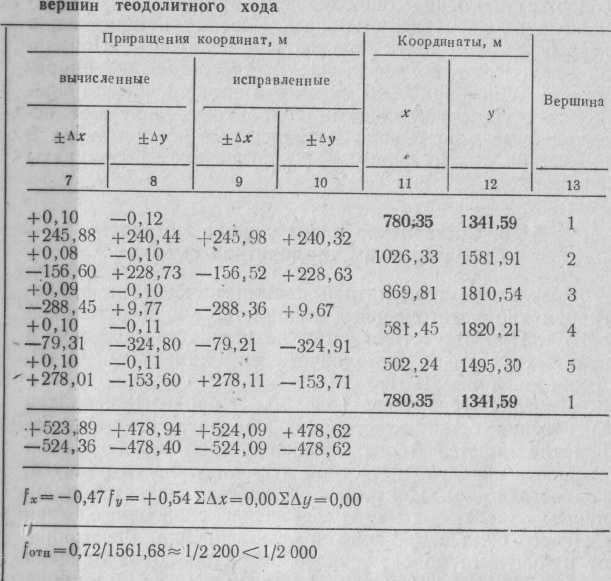
Дирекционные углы сторон хода вычисляют по (5); от них при необходимости переходят к румбам. Приращения координат Δx и Δy вычисляют по (6) на микрокалькуляторах, автоматически выполняющих тригонометрические операции. По вычисленным приращениям находят линейную невязку ходов f_L (см. § 26). При аналитическом определении положения точек хода, которое мы рассматриваем, получают не саму невязку, а ее проекции f_x и f_у на оси координат (см. рис. 53, б). Это — невязки в приращениях координат. Каждую из них находят как разность между суммой вычисленных (практически полученных) приращений и ее теоретическим значением.

Найдем теоретическое значение суммы приращений координат. Зная координаты начальной точки В (х₀, y_о) и конечной точки С (х_п, y_п) разомкнутого хода (см. рис. 67, б)и приняв измерения безошибочными, напишем уравнения для вычисления координат точек 1, 2, ..., nхода:

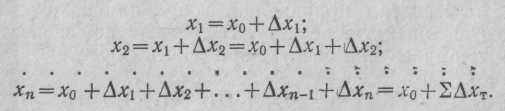
Из последнего уравнения находим ΣΔx_T = x_n—x_о- Аналогично Σ Δy_T = у _n—y _о. Следовательно,

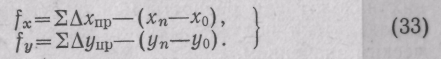
В замкнутом ходе начальная (исходная) точка является и его конечной точкой, т. е. x_n — x_o= 0; у_п — y_о = 0. Поэтому невязки вприращениях координат этого хода

По невязкам приращений координат находят абсолютную линейную невязку. В соответствии с рис. 53, б для ее вычисления следует применять формулу

В добротности выполненных измерений убеждаются по относительной линейной невязке, вычисляемой по формуле

где L — периметрхода.

Относительная невязка не должна превышать величину, определенную для данного хода по формуле (30). Если невязка допустима, вычисленные приращения исправляют. Невязки f_x и f_y распределяют так, чтобы поправки и приращения были пропорциональны длине сторон и имели знак, противоположный знаку невязки. Это правило обосновывается тем, что длинные стороны измеряются с большими погрешностями, чем короткие. Следовательно, вычисленные по ним приращения координат, какой бы величины они ни были, содержат большие ошибки, чем приращения, вычисленные по коротким сторонам. Поэтому и поправки в первые должны быть больше, чем во вторые. Поправки записывают в графах над соответствующим приращением. Алгебраически суммируя вычисленные приращения с соответствующими поправками, получают исправленные приращения и записывают их в графах 9 и 10 табл. 8. По формуле (7) вычисляют координаты вершин хода.

Составление плана участка местности по материалам теодолитной съемки

Результаты теодолитной съемки наносят на заблаговременно изготовленные планшеты с прямоугольной сеткой. При отсутствии сетки на планшете ее строят в полевых условиях металлическими линейками Ф. В. Дробышева или ЛБЛ.

Линейка Дробышева (рис. 70, а) предназначена для построения сетки со стороной квадрата 10 см. В ее полотне имеется 6 окон. Рабочий край каждого окна скошен и представляет собой дугу окружности радиуса, кратного 10 см. Центром окружностей является нуль-пункт линейки — точка пересечения скошенного края нулевого окна с продольной осью линейки. Расстояние от нульпункта до скошенного ребра на конце линейки равно 70,711 см (диагональ квадрата со стороной 50 см).

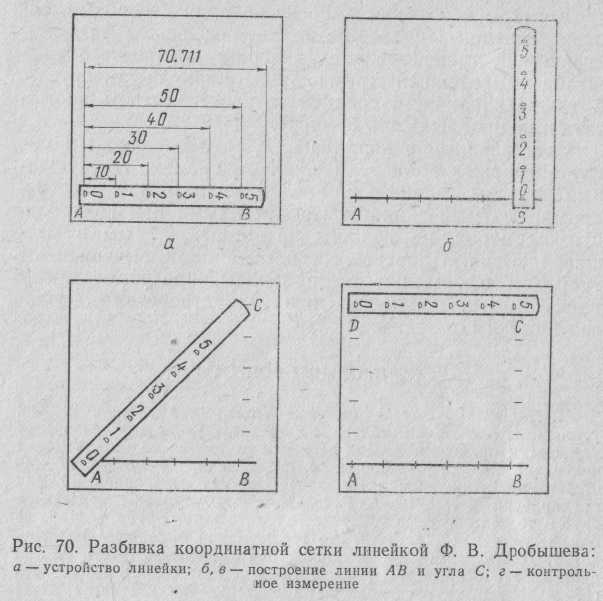Порядок разбивки сетки этой линейкой следующий: на планшете проводят (рис. 70, б) прямую, примерно параллельную его краю; накладывают линейку на нее так, чтобы она проходила через метки, поставленные на продольной оси линейки; по скошенным краям крайних окон отмечают точки A и B — вершины большого (50-сантиметрового) квадрата; из точек В и А последовательно откладывают сторону и диагональ этого квадрата так, чтобы они пересекались; в пересечении получают вершину С большого квадрата; аналогично находят вершину D; через окна в линейке разбивают стороны большого квадрата на отрезки по 10 см и проводят прямые через точки деления.

Линейка ЛБЛ устроена по принципу предыдущей, но она предназначена для разбивки сетки квадратов со стороной 8 см. В описанном выше порядке строят большой квадрат со стороной 32, 40 или 48 см (в зависимости от размеров будущего плана) и прочерчивают на его внешних сторонах через вырезы в корпусе линейки засечки через 8 см. С помощью штангенциркуля, входящего в комплект линейки, стороны большого квадрата можно разбить также на отрезки по 10 и 4 см. Линии прямоугольной сетки подписывают, руководствуясь величинами координат точек съемочного обоснования. При оцифровке линий следят за тем, чтобы план размещался по возможности симметрично относительно сторон листа бумаги. Точки съемочного обоснования наносят на план по их координатам (см. § 8). Правильность накладки двух соседних точек проверяют по горизонтальному расстоянию между ними. Расхождение между расстояниями, измеренными на плане и на местности, должно быть не больше 0,3 мм·M (M — знаменатель масштаба плана).

Контуры и объекты наносят на план способами, соответствующими способам их съемки; используют геодезический транспортир с графиком поперечного масштаба, выверенный треугольник, циркуль-измеритель, а также карандаши средней твердости (чтобы не мазать и не продавливать бумагу).

Составленный в карандаше план проверяют в поле, где оценивают полноту и точность съемки. Пропущенные контуры доснимают. Расхождения между расстояниями, взятыми с плана и полученными при контрольных промерах, не должны превышать 0,7 мм в масштабе плана. Проверенный в поле план вычерчивают тушью и оформляют по правилам, предусмотренным инструкциями по проведению лесоустройства и топографическим съемкам.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назовите этапы и процессы теодолитной съемки. 2. Как устроен теодолит? Объясните принципиальную схему измерения углов этим прибором. 3. Для чего нужны уровни на геодезических приборах? Как они устроены? 4. Какие приборы применяют для отсчета по стеклянным и металлическим кругам теодолитов? Как эти приборы устроены? 5. Расскажите об устройстве зрительной трубы теодолита. 6. Как привести зрительную трубу в рабочее положение и как убедиться, что все действия выполнены правильно? 7. Дайте определение визирной оси зрительной трубы. 8. Как проверяют и исправляют уровень на алидаде горизонтального круга? 9. Объясните расположение в зрительной трубе сетки нитей и способы проверки ее положения. 10. Назовите требования к положению визирной оси зрительной трубы, способы выявления и устранения коллимационной ошибки. П. Как измеряют теодолитом отдельный горизонтальный угол и контролируют правильность измерений? 12. Каким способом измеряют углы на точках, из которых исходят 3 и более направления? 13. Назовите точность центрирования теодолита и установки вех. 14. Какие требования учитывают при проектировании теодолитных ходов? 15. В каких случаях применяют замкнутые и разомкнутые теодолитные ходы при лесной съемке? 16. Для чего выполняют рекогносцировку хода? 17. В каком порядке и с какой точностью измеряют горизонтальные углы в теодолитных ходах? Как контролируют правильность угловых измерений? 18. Какими приборами измеряют расстояния при про-ложении теодолитного хода? Как проверяют правильность измерений? 19. Какими способами снимают подробности местности при теодолитной съемке? 20. В каком порядке выполняется математическая обработка результатов измерений в теодолитном ходе? 21. Как определяют угловую и линейную невязки в теодолитных ходах? Какие невязки считаются допустимыми? 22. Какими принципами руководствуются при введении поправок в угловые и линейные измерения теодолитного хода? 23. Какими приборами и в каком порядке разбивают прямоугольную сетку на планшете? 24. Расскажите о порядке нанесения на план точек съемочного обоснования и снятой ситуации.

Дата добавления: 2014-10-28; просмотров: 1979; Нарушение авторских прав

Мы поможем в написании ваших работ!