Аналитический способ определения площадей земельных участков

Способы определения площадей

СПОСОБЫ ОПРЕДЕЛЕНИЯ ПЛОЩАДЕЙ УЧАСТКОВ И ИХ ТОЧНОСТЬ

Составление различного рода проектов, связанных с использованием земельной территории, изучение ее природных богатств, учет и инвентаризация земель требуют определения площадей.

При проведении этих работ определяют небольшие площади строений, сооружений, уличных проездов, площадей, парков, усадебных участков, огородов и большие площади – городов или сельских населенных пунктов, целых землепользований и севооборотных массивов.

Наряду с величиной площади требуется знать и точность ее определения. В зависимости от хозяйственной значимости участков и массивов, их размеров, конфигурации и вытянутости, наличия результатов измерения линий и углов на местности и планово-картографического материала, а также топографических условий местности применяются следующие способы определения площадей.

1. Аналитический: площадь вычисляется по результатам измерений линий и углов на местности или по их функциям – координатам вершин фигур.

2. Графический: площадь вычисляют по результатам измерений линий и углов (транспортиром) или по координатам точек на плане (карте).

3. Механический: площади определяют на плане при помощи специальных приборов (планиметров, картометров) и приспособлений (палеток, ротометров). Нередко эти способы применяют комбинированно.

Например, часть линейных величин для вычисления определяют по плану, а часть — по результатам измерений на местности. Нередко основную площадь участка, заключенного в теодолитный полигон, определяют аналитическим способом (по координатам вершин полигона), а площадь, выходящую за пределы полигона и заключенную между линиями полигона и эго урочища (серединой ручья, берега реки), — графическим или механическим способом.

Если по результатам измерений на местности определены координаты вершин замкнутого многоугольника, то его площадь может быть определена аналитическим способом.

Пусть известны прямоугольные координаты вершин треугольника 1-2-3 (рис. 4.1). Опустив из его вершин перпендикуляры на ось 0у, площадь треугольника S можно представить следующим образом:

S = S_I + S_II + S_III,

где – S_I, S_II, S_III - площади трапеций соответственно I – (1¢ - 1 – 2 – 2¢), I I – (2¢ - 2 – 3 – 3¢) и III – (1¢ – 1 – 3 – 3¢).

Площади рассматриваемых трапеций определяются как:

S_I=1/2(x₁+x₂)(y₂-y₁);

S_II=l/2(x₂+x₃)(y₃-y₂);

S_III=l/2(x_l+x₃)(y₃-y₁).

Тогда удвоенная искомая площадь треугольника 1 – 2 – 3 будет равна

2S = (х1 + х2 )(у2 – у1 ) + (х2 + х3 )(у3 - у2 ) – (x1 + х3 )(у3 - у1),

или

2S = (х1 + х2 )(у2 – у1 ) + (х2 + х3 )(у3 - у2 ) + (x1 + х3 )(у1 – у3).

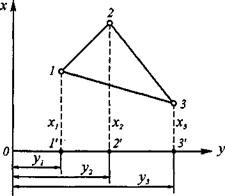
Рис. 4.1. Аналитический способ определения площади

После раскрытия скобок, соответствующей группировки членов уравнения и вынесения за скобки общих знаменателей получим

2S = X₁(Y₂ – Y₃) + X₂(Y₃ – Y₁) + X₃(Y₁ – Y₂),

или

2S = Y₁(X₃ – X₂) + Y₂(X₁ – X₃) + Y₃(X₂ – X₁).

В общем виде

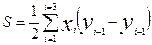, или ,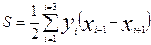

Тогда для многоугольника с числом вершин n при их оцифровке по ходу часовой стрелки формулы общего вида запишутся так:

; ,

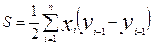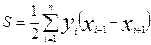где i = 1, 2, 3 . . . n.

Для контроля вычисления производят по обеим формулам.

На практике для вычисления площадей полигона удобно использовать формулы, в которые наряду с координатами точек входят приращения координат. Это позволяет вести вычисления непосредственно в ведомости вычисления координат, в которой имеются все элементы, входящие в формулу.

В общем виде можно записать

.

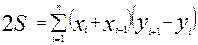Поскольку 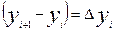, то

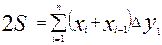
или

.

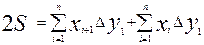Пример расчета площади по координатам точек полигона и приращениям координат приведен в табл. 4.1.

Таблица 4.1. Результаты вычисления площади в пределах теодолитного полигона

N точек	Исправленные приращения, м	Координаты, м	±	Dухi+1 м2	±	Dуiхi м2	±	DуiDхi м2
	±	Dх	±	Dу	±	X	±	У
					+	6327,12	+	3741,10
	+	116,50	+	79,36					+		+		+
					+	6443,62	+	3820,46
	-	163,79	+	354,72					+		+		-
				+	6279,83	+	4175,18
	-	30,30	-	351,32					-		-		+
				+	6249,53	+	3823,86
	-	59,66	-	141,47					-		-		+
					+	6189,87	+	3682,39
	+	137,25	+	58,71					+		+		+
					+	6327,14	+	3741,10
								S	+		+		-

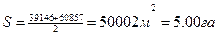
В рассматриваемом случае точность вычисления площади определяется лишь погрешностями угловых и линейных измерений на местности. Так, при измерении углов с точностью 1¢ и длин линий с точностью 1:2 000 относительная погрешность определения площади составит примерно 1:1 500.

При определении площадей сложной конфигурации с большим числом вершин вычисления рекомендуется проводить с использованием ЭВМ.

Дата добавления: 2014-02-28; просмотров: 5049; Нарушение авторских прав

Мы поможем в написании ваших работ!