
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вычисление площадей плоских фигур
1 случай. Функция 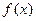 неотрицательна и непрерывна на [a, b].
неотрицательна и непрерывна на [a, b].
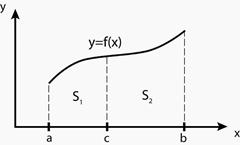
Тогда по геометрическому смыслу определённого интеграла площадь S под кривой 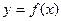 на
на 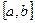 численно равна определённому интегралу:
численно равна определённому интегралу:
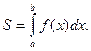
2 случай. Функция 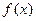 неположительна и непрерывна на
неположительна и непрерывна на 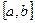 . Тогда площадь над кривой
. Тогда площадь над кривой 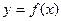 на
на 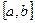 равна
равна

3 случай. Функция 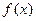 общего вида на
общего вида на 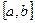 . Пусть исходный отрезок можно разбить на конечное число интервалов, в каждом из которых
. Пусть исходный отрезок можно разбить на конечное число интервалов, в каждом из которых 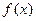 имеет постоянный знак или равна нулю:
имеет постоянный знак или равна нулю:
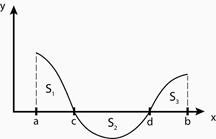
Тогда площадь фигуры равна

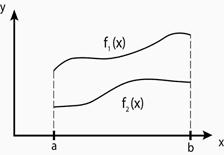
4 случай. Теорема. Пусть на 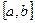 заданы непрерывные функции
заданы непрерывные функции 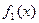 и
и  ,
,  Тогда площадь фигуры между кривыми
Тогда площадь фигуры между кривыми 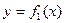 и
и  на
на 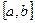 равна
равна

Вычисление объёмов тел вращения.
Пусть на 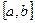 задана непрерывная знакопостоянная функция
задана непрерывная знакопостоянная функция 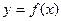 . Найдём
. Найдём 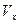 тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями
тела, образованного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями 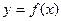 ,
,  ,
,  ,
,  .
.

Разобьем 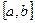 на элементарные отрезки точками
на элементарные отрезки точками  и на каждом
и на каждом 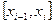 некоторым образом выберем
некоторым образом выберем 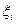 , где
, где 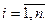 Тогда приближённое значение для объёма выражается формулой:
Тогда приближённое значение для объёма выражается формулой:
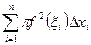 ,
,
где каждое слагаемое – это объём цилиндра с высотой 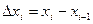 и радиусом
и радиусом 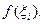 Это приближение тем лучше, чем меньше
Это приближение тем лучше, чем меньше  , поэтому перейдём к пределу
, поэтому перейдём к пределу
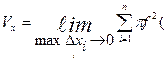
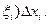
В правой части – интегральная сумма для функции  , поэтому
, поэтому
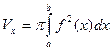
По аналогии можно записать формулу для объёма тела, образованного вращением вокруг оси  криволинейной трапеции, образованной линиями
криволинейной трапеции, образованной линиями 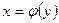 ,
, 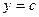 ,
,  ,
,  :
:
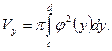
| <== предыдущая страница | | | следующая страница ==> |
| Формула Ньютона-Лейбница | | | Несобственные интегралы |
Дата добавления: 2014-02-28; просмотров: 716; Нарушение авторских прав

Мы поможем в написании ваших работ!