Формула Ньютона-Лейбница

Теорема. Пусть функция 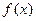непрерывна на [a, b] и F(x) – любая первообразная для 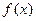на [a, b]. Тогда

Это формула Ньютона-Лейбница.

Находятся определённые интегралы с помощью формулы Ньютона-Лейбница в два шага: на первом шаге находят первообразную F(x) для 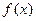, а на втором – применяется формула Ньютона-Лейбница. Применяются обозначения:

Пример.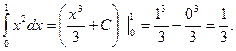

Значение С в данном случае несущественно, поэтому его принимают равным нулю.

Замена переменной и формула интегрирования по частям в определённом интеграле.

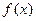Теорема. Пусть функция имеет непрерывную производную на и функция непрерывна в каждой точке . Тогда справедливо равенство

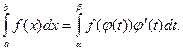
Эта формула называется формулой замены переменной в определённом интеграле.

Пример. Замена 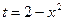; тогда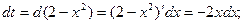 Заменим пределы интегрирования: при х=0 t=2; при x=1 t=1, следовательно

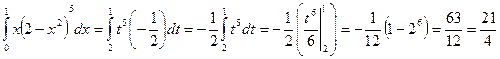
Теорема. Пусть функция u=u(x) и v=v(x) непрерывно дифференцируемы на [a, b], тогда

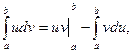
где

Эта формула называется формулой интегрирования по частям для определённого интеграла.

Геометрические приложения определённого интеграла.

Дата добавления: 2014-02-28; просмотров: 549; Нарушение авторских прав

Мы поможем в написании ваших работ!