Повторные испытания. Формула Бернулли

Лекция 3. Формула полной вероятности. Формула Байеса.

3.1. Формула полной вероятности.Пусть некоторое событие А может наступить при появлении одного из несовместимых событий 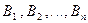– образуют полную группу. Тогда справедлива формула полной вероятности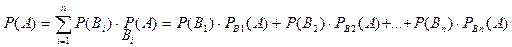

Доказательство: по условию А может наступить, если наступит одно из несовместных событий 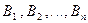, поэтому А может быть представлено 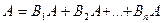. Поэтому вероятность А равна сумме вероятностей этих событий. События 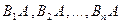–несовместны.

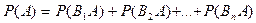
События B₁ и A, B₂ и A,... B_n и A – события совместимые, поэтому , , .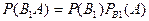

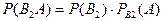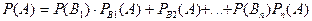3.2. Формула Байеса.

Будем считать, что событие А может наступать при появлении одного из несовместимых событий. 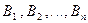–образуют полную группу, но заранее не известно, какое из событий 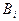наступает, поэтому 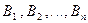называют гипотезами. Формула Байеса позволяет переоценить вероятность гипотез, после того, как результат эксперимента известен. Поскольку 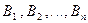–несовместны, то для события А справедлива формула полной вероятности. Формула Байеса имеет вид: .

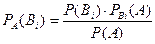Доказательство: Так как события 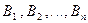–несовместимы и образуют полную группу, то .

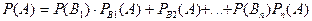Вероятность совместного наступления2 событий 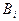и А–вероятность произведения ;

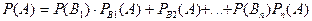где 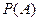находится по формуле полной вероятности.

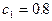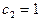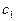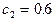Пример: при отклонении от нормального режима работы автомата, срабатывает сигнализация и . Вероятность того, что автомат снабжен сигнализацией или и 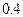. Получен сигнал о том, что автомат остановился. Что вероятнее: автомат снабжен 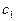или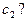

Решение: А – сигнал получен,

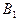– автомат снабжен сигнализацией С₁.

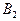– автомат снабжен сигнализацией С₂.

Найти: .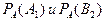

, .

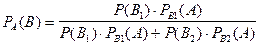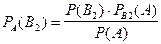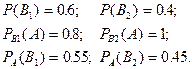
Вероятность того, что автомат снабжен сигнализацией С₁.

3.3. Повторные испытания. Формула Бернулли.

Повторными испытаниями называется ряд опытов, проведенных при одних и тех же условиях. Независимыми испытаниями называются также испытания, в каждом из которых событие А наступает независимо от других испытаний.

Пусть А – противоположное, .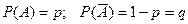

Формула Бернулли имеет вид: .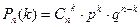

С помощью формулы находим, что в n испытаниях событие наступает k раз.

Доказательство: Вероятность сложного события состоит в том, что событие А наступает k раз и не наступает n-k раз. По теореме умножения вероятности независимых событий получаем 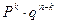. Всего этих событий было 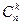, поэтому 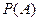вычисляется по формуле Бернулли.

Замечание: вероятность достоверного события равна 1.

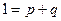, используя биномиальное разложение 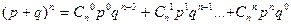, 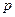–вероятность наступления события в единичном испытании, 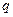–противоположное событие.

Так как по формуле Бернулли вероятность того, что в 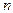испытаниях 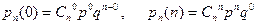, то .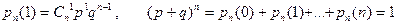

Определение. Дискретной, случайной величиной, называется случайная величина, принимающая отдельные, изолированные значения.

Определение. Законом распределения дискретной случайной величины называется перечень значений случайной величины, их вероятность. Вероятности, вычисленные по формуле Бернулли, дают биномиальные распределения.

Пример. Производятся выстрелы. 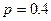–вероятность попадания при одном выстреле.

Найти вероятность того. Что при 6 выстрелах будут все промахи, 1 попадание, 2, 3, и т.д. Построить кривую распределения.

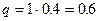
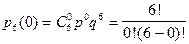
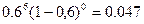
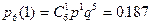
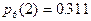
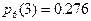
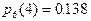
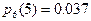
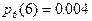
Поскольку эти события образуют полную группу, то .

Полученный график называется многоугольником вероятности или полигоном вероятности.

Дата добавления: 2014-02-26; просмотров: 1497; Нарушение авторских прав

Мы поможем в написании ваших работ!