
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Повторные независимые испытания. Вероятность наступления события при независимых испытаниях (формула Бернулли). Наивероятнейшая частота
Пусть проводится n испытаний, в каждом из которых событие А может произойти или не произойти, причем вероятность события А от испытания к испытанию не меняется. Такие испытания называются независимыми. В противном случае испытания зависимы. Вероятность наступления события А при каждом испытании обозначим р, то есть P(A)=p, тогда  .
.
При n независимых испытаниях событие А практически может наступить любое число раз (m раз) в разных комбинациях с противоположным событием 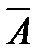 (которое может наступить (n-m) раз).
(которое может наступить (n-m) раз).
Рассмотрим простейшую комбинацию:
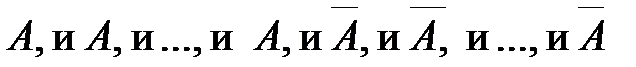 , то есть событие А наступает m раз подряд, а затем
, то есть событие А наступает m раз подряд, а затем  раз наступает событие
раз наступает событие  . Используя теорему умножения вероятностей независимых событий, получим
. Используя теорему умножения вероятностей независимых событий, получим 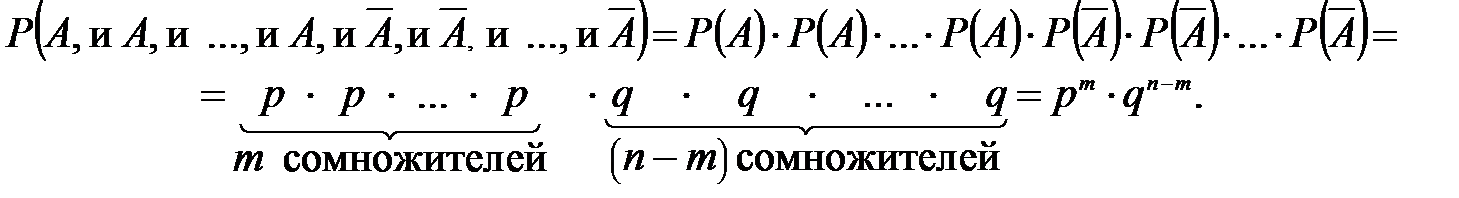
Различных комбинаций, в которых событие А наступает m раз, всего будет 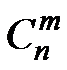 , вероятность наступления каждой из этих комбинаций одинаковая и равна
, вероятность наступления каждой из этих комбинаций одинаковая и равна 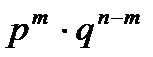 .
.
Вероятность наступления события А m раз при n испытаниях символически записывается так:  .
.
Итак, 
Таким образом,  .
.
Полученная формула называется формулой Бернулли.
Наивероятнейшая частота
Частота m0 называется наивероятнейшая частота, если выполняются одновременно 2 условия
Рm0 ,n (A) ≥ Рm0 - 1,n (A)
Рm0 ,n (A) ≥ Рm0 + 1,n (A)
1)  *pm0*qn-m0≥
*pm0*qn-m0≥  *pm0-1*qn-m0+1
*pm0-1*qn-m0+1
2)  *pm0*qn-m0≥
*pm0*qn-m0≥  *pm0+1*qn-m0-1
*pm0+1*qn-m0-1
Разделим 1 на pm0-1qn-m0, a 2 на pm0 qn-m0-1
 p≥
p≥  q
q
 ≥
≥  p
p
1) 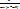 p≥
p≥  q
q
2) 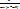 q≥
q≥ 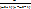 p
p
Домножаем 1 на 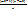 , 2 на
, 2 на 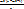
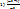 p≥
p≥  q
q
2)  q≥
q≥  p
p
 p≥
p≥  q
q
 ≥
≥ 
1)  ≥
≥  домножаем на m0
домножаем на m0
2)  ≥
≥  домножаем на m0+1
домножаем на m0+1
1)p≥ 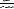 домножаем на (n-m0+1)
домножаем на (n-m0+1)
2)  ≥ p домножаем на (n-m0)
≥ p домножаем на (n-m0)
1) (n-m0+1)p≥qm0
2) (m0+1)q≥(n-m0)p
1) np-m0p+p-qm0≥0
2) m0q+q-np+m0≥0
1) np+p-m0(p+q)≥0
2)q-np+m0(p+q)≥0
np+p≥m0
m0≥np-q
np-q≤ m0 ≤ np+p формула наивероятнейшей частоты
| <== предыдущая страница | | | следующая страница ==> |
| Вероятность гипотез (формула Байеса) | | | Теорема Пуассона |
Дата добавления: 2014-09-01; просмотров: 1477; Нарушение авторских прав

Мы поможем в написании ваших работ!