Вероятность случайного события

Событие – появление определенного признака, например, заданного числа частиц газа в единице объема около выбранной точки. Вероятность признака равна относительному числу его появления.

Пример. Для газа в сосуде концентрация частиц около точки r есть число частиц в единице объема около r

,

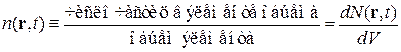изменяется с течением времени хаотически.

Событие – наблюдение определенной концентрации .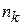

Проводим N измерений концентрации, результат 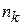наблюдается раз, тогда вероятность результата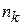

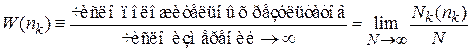. (1.1)

Область определения вероятности ограничена интервалом

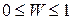
между невозможным 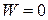и достоверным 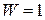событиями. Зависимость 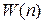называется функцией распределения вероятностисобытий. Например, при бросании симметричной игральной кости, имеющей 6 граней, вероятность выпадения какой-либо определенной грани равна 1/6 и распределение вероятности равномерное.

Несовместимые события А₁, А₂,…, А_k не могут произойти одновременно. Например, если бросать шестигранную кость, на каждой грани которой написано число от 1 до 6, можно получить результат: или 1, или 2,…, или 6. Выполняется теорема сложения вероятностей несовместимых событий – вероятность сложного события A или B равна сумме вероятностей отдельных событий. Действительно, выполняется

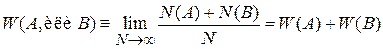. (1.2)

Если (А₁, А₂,…, А_k) – полный набор несовместимых событий, то какое-либо одно из них обязательно происходит, тогда выполняется

.

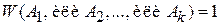С учетом (1.2) получаем условие нормировки вероятностей для полного набора несовместимых событий

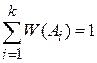. (1.3)

Пример. Движения молекулы газа по и против некоторой оси образуют полный набор независимых направлений движения

W(влево) + W(вправо) = 1.

Если у гамильтониана системы все направления равноправные, тогда

W(влево) = W(вправо) = 1/2.

Независимые события А₁, А₂,…, А_k не влияют друг на друга. Например, частицы идеального газа движутся независимо друг от друга, и положение одной частицы не влияет на положение другой частицы. Выполняется теорема об умножении вероятностей независимых событий – вероятность сложного события А и B равна произведению вероятностей отдельных событий

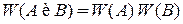, (1.4)

Для k независимых событий

.

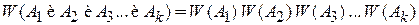Пример. В объеме V₀, все точки которого равноправные, находится частица. Объем V₀ разбиваем на N одинаковых ячеек объемом 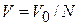. При обследовании всех ячеек, т.е. при 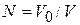измерениях, положительный результат будет только в одной ячейке. Вероятность найти частицу в одной произвольной ячейке согласно (1.1)

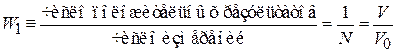. (1.4а)

Если в V₀ находится m независимых частиц, то вероятность, что весь газ окажется в объеме V, согласно теореме (1.4) равен

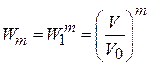. (1.4б)

Дата добавления: 2014-02-27; просмотров: 473; Нарушение авторских прав

Мы поможем в написании ваших работ!