Вероятность занятия серверов. Нам необходимо найти вероятность занятия определенных, выбранных заранее серверов

Нам необходимо найти вероятность занятия определенных, выбранных заранее серверов. Эта задача часто встречается при определении нагрузки на определенные выходы в коммутаторах каналов телефонных сетей. В результате применения модели Эрланга или Энгсета или Бернулли найдены вероятности занятия любых k серверов p_k .

Зафиксируем определенные i серверов из m доступных. Предположим, что занятие серверов происходит равновероятно. Тогда если в системе с вероятностью 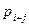занято точно i + j серверов, то вероятность занятия одной конкретной комбинации будет в число таких сочетаний раз меньше, т.е..

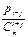Поскольку отмеченные i серверов могут быть заняты совместно с любыми другими j серверами в соответствующем числу сочетаний из m по j комбинациях, где j любое число от 0 до m-i , то можно получить формулу для вероятности занятия фиксированных i серверов в системе с M входами:

.

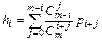Для модели Эрланга тогда получим:

.

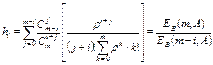Длямодели Энгсетаформула будет отличаться:

.

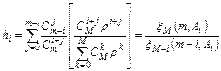Для системы с одинаковым числом входов и выходов (серверов) имеет место модель Бернулли и соответствующие вероятности занятия фиксированных серверов будут:

.

Дата добавления: 2014-03-13; просмотров: 495; Нарушение авторских прав

Мы поможем в написании ваших работ!