
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Зависимые и независимые события
Определение. (Условной вероятности) Условной вероятностью называется вероятность события 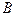 , вычисленная в предположении , что событие
, вычисленная в предположении , что событие 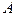 уже наступило.
уже наступило.
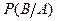 или
или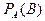
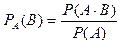
Теорема 2.2.(Об умножении вероятностей двух совместных событий) Вероятность совместного появления двух событий равно произведению вероятностей одного из них , умноженную на условную другого.
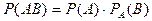 , при условии , что событие А произошло.
, при условии , что событие А произошло.
По определению условной вероятности 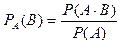 , следует
, следует 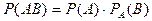
Обобщение теоремы 2.2.Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности остальных, где каждая условная последующая вероятность вычисляется в предположении, что все предыдущие события наступили.
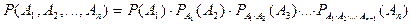
Следствие 1. ( О произведении вероятностей независимых событий ) Пусть события А и В независимы, тогда вероятность всех совместных событий равна произведению вероятностей тех событий.
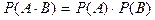
События называются независимыми в совокупности или просто независимыми, если они попарно независимы.
Следствие 2. Вероятность совместного появления независимых событий 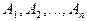 равна произведению вероятностей этих событий:
равна произведению вероятностей этих событий:
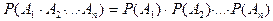
Теорема 2. 3. ( О вероятности появления хотя бы одного из независимых событий) Пусть события 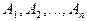 независимы в совокупности, тогда вероятность появления хотя бы одного из них вычисляется по формуле :
независимы в совокупности, тогда вероятность появления хотя бы одного из них вычисляется по формуле : 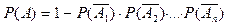 .
.
Доказательство: пусть А - событие , состоящее в появлении хотя бы одного из событий 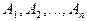 . Событию А противоположным является событие
. Событию А противоположным является событие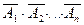 , следовательно
, следовательно
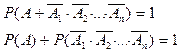
Замечание. Если обозначим 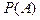 через
через 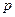 , а
, а 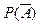 через
через 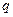 , то
, то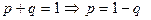
Если все события 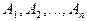 независимы и равновозможны ( все их вероятности одинаковы) , тогда вероятность появления хотя бы одного события
независимы и равновозможны ( все их вероятности одинаковы) , тогда вероятность появления хотя бы одного события 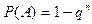 , где
, где
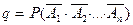 .
.
Пример. В студии имеется три камеры. Вероятность быть включенной для каждой составляет 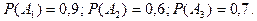 Найти вероятность того, что в данное время будет:
Найти вероятность того, что в данное время будет:
1.) включена хотя бы одна камера ( событие А );
2.) включены все три камеры ( событие В );
3.) включена точно одна камера ( событие С ).
Решение:
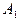 - включена первая камера ,
- включена первая камера ,
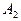 - включена вторая камера ,
- включена вторая камера ,
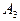 - включена третья камера .
- включена третья камера .
1.) 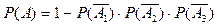 =1 - 0.012 = 0.988
=1 - 0.012 = 0.988
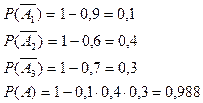
2.) 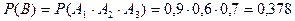
3.) 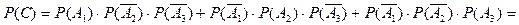
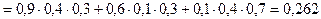
Теорема 2.4. ( О сложении вероятностей совместных событий ) Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного наступления.
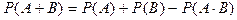
Обобщение теоремы 2.4. Пусть А,В,С - совместные события , тогда вероятность их суммы равна:
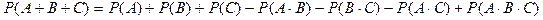
Пример. Среди 25 билетов 5 хороших. 3 судента наудачу вытащили по одному билету. Найти вероятность того, что все 3 студента вытащили хорошие билеты.
А1 – первый студент вытянул хороший билет.
А2 – второй студент вытянул хороший билет.
А3 – третий студент вытянул хороший билет.
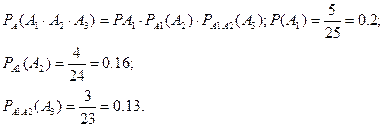
(Доказательство по т.2.4.).
События А1+А2+А3 представим в виде (А1+А2)+А3, тогда 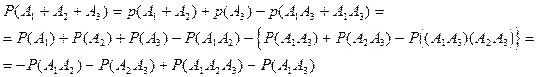
| <== предыдущая страница | | | следующая страница ==> |
| Объединение, пересечение событий. Противоположные события | | | Повторные испытания. Формула Бернулли |
Дата добавления: 2014-02-26; просмотров: 1155; Нарушение авторских прав

Мы поможем в написании ваших работ!