Зависимые и независимые события. Условная вероятность события

События называются независимыми, если при данном испытании наступление одного события не изменяет вероятности наступления других, в противном случае события будут зависимыми.

Условной вероятностью РА(В) называется вероятность события В, вычисленная в предположении, что событие А уже произошло.

Для независимых событий А и В условная вероятность равна безусловной, то есть 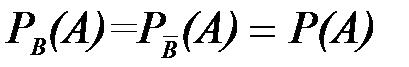и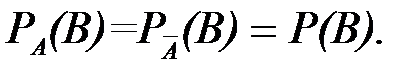

Теорема1: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое уже произошло, т.е. Р(АВ)= Р(А)РА(В).

Доказательство:

Пусть в результате опыта возможны N исходов, из них М благоприятствуют появлению события А, их этихМ- К исходов благоприятствуют событию В. Одновременному появлению событий А и В благоприятствуют L исходов из К.. По классической формуле имеем: Р(АВ)=L/N. Умножим и разделим на М:

Р(АВ)=M/N *L/M

Первая дробь- вероятность наступления события А, вторая- вероятность события В, при условии, что А уже произошло, т.е. условная вероятность события В, что и требовалось доказать.

Теорема2: Вероятность произведения двух независимых событий А и В равна произведению их вероятностей Р(АВ)=Р(А)Р(В).

Доказательство:

Т.к. события независимые, то верно равенство РА(В)=Р(В), тогда получим Р(АВ)=Р(А)Р(В).

Справедлива обратная теорема:

Если для событий А и В выполняется равенство Р(АВ)=Р(А)Р(В), то эти события независимы.

Дата добавления: 2014-09-01; просмотров: 553; Нарушение авторских прав

Мы поможем в написании ваших работ!