
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Теорема сложения вероятностей для несовместных событий и следствия из нее
Вероятность появления какого-либо из нескольких несовместных событий равна сумме вероятностей этих событий, то есть
Р (А1, или А2, или ..., или Аn) = Р(А1) + Р(А2) + ...+Р(Аn).
Доказательство. Докажем теорему вначале для двух несовместных событий А и В. Пусть N - общее число единственно возможных, равновозможных и несовместных исходов. Из них М1 исходов благоприятствуют событию А, а М2 - событию В.
Тогда Р(А) =M1/N, Р(В) = M2/N.
По условию задачи, события А и В несовместны. Следовательно, ни один из М1 исходов, благоприятствующих событию А, не благоприятствует событию В. И наоборот, ни один исход из М2 не благоприятствует событию А. Отсюда следует, что сумме событий А+В (А или В) благоприятствует (М1+М2) исходов из N, а поэтому
P(A или B)=(M1+M2)/N
Последнее равенство можно записать так:
P(A или B) Р(А)+Р(В) = M1/N + M2/N
Итак, для двух несовместных событий теорема доказана. Применяя метод математической индукции, докажем справедливость теоремы для любого конечного числа несовместных событий.
Допустим, что теорема справедлива для n несовместных событий, то есть
Р (А1, или А2, или ..., или Аn) = Р(А1) + Р(А2) + ...+Р(Аn).
Докажем, что она справедлива и для (n+1) событий. Сумму событий (А1, или А2, или ..., или Аn, или Аn+1) представим в виде суммы двух событий: (А1, или А2, или ..., или Аn ) или Аn+1 . Применяя теорему сложения вероятностей для двух несовместных событий, будем иметь
P(А1, или, А2 или …, или А n, или A n+1)=
= P((А1, или А2, или …, или Аn), Аn+1 или)=
= P(А1, или А2, или …, или Аn)+P(Аn+1).
Так как для n событий мы предположили, что теорема справедлива, то получим
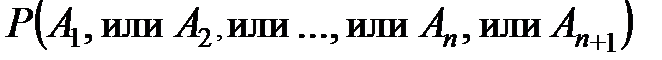
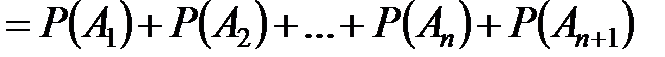 ,
,
что и требовалось доказать.
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице.
Доказательство. События А1, А2, ..., Аn образуют полную группу событий. Следовательно, с одной стороны, эти события единственно возможные (наступит хотя бы одно из них), а поэтому их сумма является достоверным событием, его вероятность равна единице, то есть
Р(А1, или А2, или ..., или Аn )=1.
С другой стороны, события А1, А2, ..., Аn - несовместные. Тогда по теореме сложения вероятностей имеем
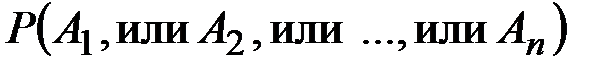 =
= 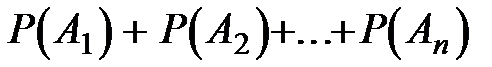 .
.
Объединяя два последних равенства, получаем
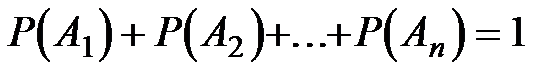 ,
,
что и требовалось доказать.
Следствие 2. Сумма вероятностей двух противоположных событий равна единице.
Доказательство. Противоположные события А и 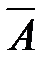 образуют полную группу событий. Тогда на основании следствия 1 имеем
образуют полную группу событий. Тогда на основании следствия 1 имеем
Р(А) + Р( 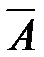 )=1.
)=1.
Замечание. Следствие 2 часто используется при решении задач. Это связано с тем, что иногда проще рассчитать вероятность противоположного события 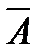 , а не события А. В таких случаях сначала вычисляют Р(
, а не события А. В таких случаях сначала вычисляют Р( 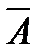 ), а затем находят Р(А) =1 - Р(
), а затем находят Р(А) =1 - Р( 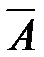 ).
).
| <== предыдущая страница | | | следующая страница ==> |
| Подъём производства накануне индустриализации | | | Зависимые и независимые события. Условная вероятность события |
Дата добавления: 2014-09-01; просмотров: 679; Нарушение авторских прав

Мы поможем в написании ваших работ!