Алгебра событий

Основные понятия

Исходными понятиями теории вероятностей являются понятия стохастического эксперимента, случайного события и вероятности случайного события.

Стохастическим назовём эксперимент, результат которого заранее (до его проведения) предугадать нельзя. Часто вместо стохастического эксперимента говорят об испытании, опыте.

Случайным событием назовем явление, которое может произойти или не произойти в результате стохастического эксперимента.

Пример.Рассмотрим опыт с бросанием игральной кости (кубик, каждая грань которого имеет метки - очки, соответствующие цифрам 1, 2, 3, 4, 5, 6). Результатом этого стохастического эксперимента/опыта может быть появление одного из чисел 1, 2, 3, 4, 5, 6, равного числу выпавших очков. Можно рассматривать и другие события, заключающиеся, например, в том, что сумма выпавших чисел равна пяти, чётная, делится на три и так далее.

Для обозначения случайных событий будем использовать большие буквы A, B, C, снабжая их при необходимости индексами.

Предположим теперь, что среди всех возможных событий, которые в данном опыте могут произойти или не произойти, можно выделить совокупность так называемых элементарных событий, которые обладают следующими свойствами:

взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий,

каково бы ни было случайное событие A, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие A.

Элементарные события будем обозначать греческой буквой w, снабжённой при необходимости индексом, а их совокупность W будем называть пространством элементарных событий.

Вернёмся к примеру. В этом случае элементарными событиями w_iможно считать появление любого числа от 1 до 6. Очевидно, что всего имеется 6 элементарных событий. Выбор элементарных событий определяется неоднозначно, чем можно пользоваться при решении задач.

Пусть W - пространство элементарных событий рассматриваемого опыта. Для каждого возможного в этом опыте события A выделим совокупность всех элементарных событий, наступление которых необходимо влечёт наступление A. Будем говорить, что эти элементарные события благоприятствуют появлению A. Множество этих элементарных событий обозначим тем же символом A, что и соответствующее событие.

Таким образом, событие A состоит в том, что произошло одно из элементарных событий, входящих в указанное множество A. Другими словами, мы отождествляем событие A и соответствующее ему множество A элементарных событий.

Введём теперь ряд понятий и определений.

Назовём событиедостоверным, если оно наступает в результате появления любого элементарного события. Но тогда ему благоприятствует любое wÎW и в силу заключённого договора будем обозначать достоверное событие тем же символом W.

Невозможнымназовёмсобытие, не наступающее ни при каком элементарном событии, но тогда ему соответствует пустое множество, и поэтому невозможное событие будем обозначать символом Æ.

Пример.В опыте с кубиком достоверным является событие, что выпадет число, меньшее 7. Невозможным – выпадет отрицательное число.

Суммой (или объединением) двух событий A и B назовём событие A + B (или AÈB), происходящее тогда и только тогда, когда происходит или A, или B. Сумме событий А и В соответствует объединение множеств А и В.

Отметим очевидные соотношения: A+Æ=A, A+W=W, A+A=A.

Пример. Событие “выпало четное” является суммой событий: выпало 2, выпало 4, выпало 6.

Произведением (или пересечением) двух событийA и B назовём событие AB (или AÇB), которое происходит тогда и только тогда,когда происходит и A, и B. Произведению событий А и В соответствует пересечение множеств A и B.

Отметим очевидные соотношения: AÆ = Æ, AW = A, AA = A.

Пример. “Выпало 5” является пересечением событий: выпало нечетное и выпало больше 3-х.

Два события назовём несовместными, если их совместное появление в одном и том же опыте невозможно. Следовательно, если A и B несовместны, то их произведение - невозможное событие: AB = Æ.

Введённые ранее элементарные события, очевидно, попарно несовместны - w_iw_j= Æ при i ¹ j.

Пример. Выпало четное число и выпало нечетное число – события несовместные.

Событие 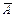назовём противоположным к 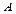, если оно происходит тогда и только тогда, когда 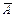не происходит.

Отметим очевидные соотношения: .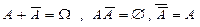

Пример. Выпало четное число и выпало нечетное число – события противоположные.

Разностью событий A и B назовём событие A\B, происходящее тогда и только тогда, когда происходит A, но не происходит B.

Отметим очевидные соотношения: .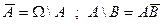

Поскольку разность событий можно выразить с помощью операций отрицания и произведения, пользоваться разностью событий в дальнейшем не будем.

Таким образом, операциям над событиями соответствуют аналогичные операции над множествами.

Введённые выше операции сложения и умножения обладают следующими свойствами:

.

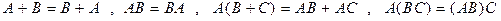Пример.Производится два выстрела по цели. Пусть событие A - попадание в цель при первом выстреле и B - при втором, тогда и - промах, соответственно, при первом и втором выстрелах. Обозначим поражение цели событием C и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить C через A и B.

Решение. Цель будет поражена в следующих случаях: попадание при первом и промах при втором; промах при первом и попадание при втором; попадание при первом и втором выстрелах. Используя введённые выше операции, перечисленные варианты можно, соответственно, записать: 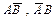и 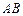. Интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть

.

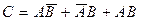С другой стороны, событие 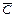, противоположное С, есть промах при двух выстрелах, то есть 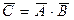, отсюда искомое событие С можно записать в виде .

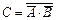Возможность различного выражения искомого события часто оказывается полезной при решении задач.

Для понимания введённых понятий полезна геометрическая интерпретация: представим пространство элементарных событий W в виде квадрата, каждой точке которого соответствует элементарное событие. Тогда случайные события будут изображаться в виде некоторых фигур, лежащих в этом квадрате.

На рис. 1.1. заштрихованные фигуры представляют:

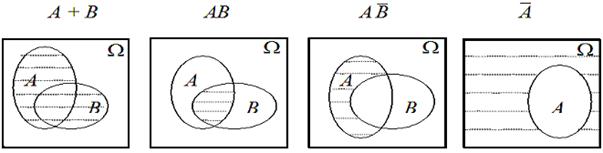
Рис. 1.1.

Рассмотрим пространство элементарных событий W, соответствующее некоторому стохастическому эксперименту, и пусть F - некоторая система случайных событий. Систему событий F назовём алгеброй событий, если выполняются условия: WÎF; из того, что AÎF, следует, что 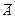ÎF; из того, что A и BÎF,следует, что AB и A + B ÎF. Отсюда следует, что, применяя любые из введённых выше операций к произвольной системе событий из F, получим событие, также принадлежащее F.

Дата добавления: 2014-03-11; просмотров: 749; Нарушение авторских прав

Мы поможем в написании ваших работ!