
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Методы решения нелинейных алгебраических уравнений
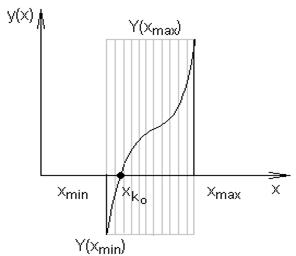 |
Метод сканирования (перебора, равномерного поиска). Суть метода состоит в том, что диапазон xmin£x£xmax разбит на n-отрезков,
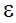 - окрестностей.
- окрестностей.
Рис.6.1. Нахождение корня методом сканирования
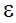 - заранее заданная точность вычисления корня (например,
- заранее заданная точность вычисления корня (например, 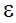 £0,001) уравнения ¦(x)=0. Вычисляются последовательно все значения ¦(xk), k=0... n. Затем из этого ряда выбирается значение ¦(xk0) , близкое к нулю. Значение xk0 будет решением уравнения с заданной точностью e.
£0,001) уравнения ¦(x)=0. Вычисляются последовательно все значения ¦(xk), k=0... n. Затем из этого ряда выбирается значение ¦(xk0) , близкое к нулю. Значение xk0 будет решением уравнения с заданной точностью e.
Метод деления пополам. На первом шаге диапазон изменения аргумента x (xmin£x£xmax ) делится пополам и определяется середина этого отрезка
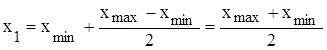 .
.
Затем определяются значения
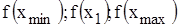 ,
,
на основе которых выбирается интервал, содержащий корень уравнения.
Выбор половинки общего интервала происходит на основании определения смены знака функции 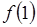 на границах, например для 1-ой половинки.
на границах, например для 1-ой половинки.
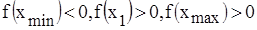 .
.
Смену знака можно определить:
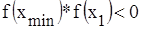 - смена знака (корень в этом поддиапазоне);
- смена знака (корень в этом поддиапазоне);
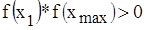 - смены знака нет (корня в этом поддиапазоне нет).
- смены знака нет (корня в этом поддиапазоне нет).
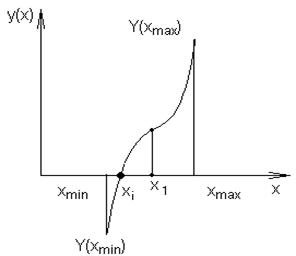
Рис. 6.2. Нахождение корня методом деления пополам
Далее эта процедура повторяется до тех пор, пока 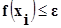 . Тогда
. Тогда 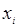 можно считать корнем уравнения вычисленного с точностью e.
можно считать корнем уравнения вычисленного с точностью e.
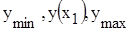 ;
; 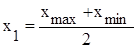 ;
;
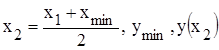 .
.
Метод золотого сечения. Метод отличается от предыдущего делением интервала на две неравные части согласно правилу золотого сечения. Золотое сечение определяется следующим образом: отношение всего отрезка к большей его части равно отношению большей части отрезка к его меньшей.
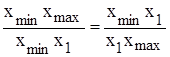 больший отрезок ближе к
больший отрезок ближе к 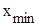
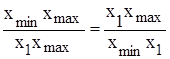 больший отрезок ближе к
больший отрезок ближе к 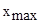
Аналитически 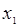 можно вычислить по следующей формуле в первом случае:
можно вычислить по следующей формуле в первом случае:
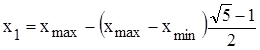 ,
,
во втором случае:
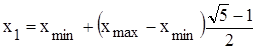 .
.
В остальном алгоритм метода золотого сечения совпадает с алгоритмом метода деления пополам. Доказано, что методу золотого сечения требуется меньше шагов (итераций) для определения корня уравнения по сравнению с многими другими методами.
Метод хорд. Суть этого метода заключается в том, что нелинейная монотонная функция 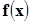 заменяется линейной в виде хорды, которую можно рассмотреть, как прямую, проходящую через две точки:
заменяется линейной в виде хорды, которую можно рассмотреть, как прямую, проходящую через две точки: 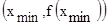 и
и 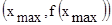 в декартовой системе координат.
в декартовой системе координат.
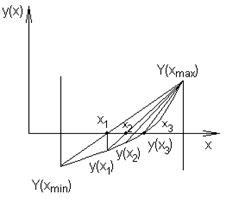
Рис. 6.3. Нахождение корня методом хорд
На основании пропорции
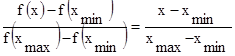
можно вывести уравнение прямой, отрезок которой является хордой:
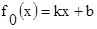 .
.
Корень x1 уравнения 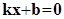 будет являться первым приближением решения нелинейного уравнения. Далее с новой точкой
будет являться первым приближением решения нелинейного уравнения. Далее с новой точкой 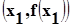 аналогично определяется точка x2 и т.д. до получения значения корня с требуемой точностью.
аналогично определяется точка x2 и т.д. до получения значения корня с требуемой точностью.
Относительно выбора концов отрезка придерживаются следующих рекомендаций: Если 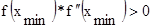 , то «закрепляется» правая точка хорды.
, то «закрепляется» правая точка хорды.
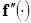 - обозначает 2ую производную функции
- обозначает 2ую производную функции 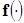 .
.
Составим уравнение касательной по двум точкам:
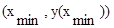 ,
,
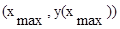 ,
,
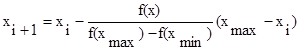 .
.
Метод касательных (Ньютона). Иллюстрация метода касательных приведена на рис.6.4.
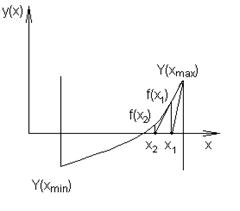 |
Рис.6.4. Нахождения методом Ньютона
Суть метода аналогична идее метода хорд, только в качестве прямой линии используется касательная, проведенная в текущей точке последовательности корней уравнения. В качестве начальной точки берется 
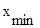 , если
, если 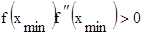 , или
, или 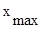 , если
, если 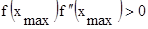 .
.
Алгоритм вычисления можно записать в следующем виде:
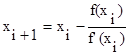 ,
,
где 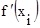 - первая производная функции
- первая производная функции 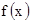 .
.
Условие окончания итерационной процедуры определяется требованием точности вычисления корня уравнения 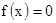
Комбинированный метод. Комбинированный метод сочетает в себе поочередное применение метода хорд и касательных. Остановка происходит, если на некотором шаге n выполняется неравенство:
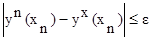 ,
,
где  - значение, определенное методом Ньютона,
- значение, определенное методом Ньютона,
либо применяется поочередная проверка:
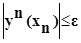
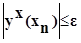 ,
,
где 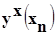 - значение, определенное методом хорд.
- значение, определенное методом хорд.
Часто используется параболическая аппроксимация вместо линейной (хорда или касательная). Алгоритм такого метода отличается только определением аппроксимационной параболы по трем точкам (боковые и середина отрезка). Соответственно, на следующем шаге решается параболическое уравнение, находится новая точка. По ней относительно концов интервалов проводится контроль смены знака функции, выбирается интервал и строится парабола и т. д. до выполнения правила остановки, определяющего момент срабатывания заданного количества шагов итераций или достижения заданной точности нахождения корня.
| <== предыдущая страница | | | следующая страница ==> |
| ЧИСЛЕННЫЕ МЕТОДЫ. Задачи математического моделирования тесно связаны с задачами решения различных уравнений или систем уравнений | | | Определение числа корней алгебраических уравнений |
Дата добавления: 2014-08-04; просмотров: 615; Нарушение авторских прав

Мы поможем в написании ваших работ!