ЧИСЛЕННЫЕ МЕТОДЫ. Задачи математического моделирования тесно связаны с задачами решения различных уравнений или систем уравнений

Задачи математического моделирования тесно связаны с задачами решения различных уравнений или систем уравнений. Уравнения можно классифицировать как линейные и нелинейные, алгебраические, трансцендентные и дифференциальные, линейные относительно коэффициентов или линейные относительно переменных. Дифференциальные уравнения подразделяются на обыкновенные и уравнения в частных производных.

Не все перечисленные классы уравнений и систем уравнений могут быть решены в явном виде, или, более корректно, в аналитической форме. Поэтому в вычислительной технике широко используются методы численного решения уравнений и систем уравнений.

Основу численных методов составляет рекурсия, т.е. вызов некоторой процедурой самой себя или многократное повторение алгоритма на данных, полученных в результате предыдущих расчетов.

Берется некоторое начальное значение (значения) в качестве нулевого приближения к искомому решению, далее производятся расчеты по некоторому алгоритму с получением следующего приближенного значения, и процедура повторяется снова до тех пор, пока не будет получена требуемая точность приближенного решения, или пока не выработается заданное количество шагов, в том случае, если алгоритм не сможет найти требуемого приближения.

Такие алгоритмы называются рекурсивными, или рекуррентными, или итерационными. Для них важными характеристиками являются сходимость, быстрота сходимости, точность полученного решения, устойчивость решения и т.д. В настоящий момент имеется достаточно большой арсенал итерационных методов, наиболее распространенные из которых рассмотрим ниже.

В качестве примера рекурсии рассмотрим ряд чисел Фибоначчи
1, 1, 2, 3, 5, 8, 13, 21.

Первые два члена этого ряда равны единице, тем самым определены начальные условия, а каждый последующий член определяется как сумма двух предыдущих:

T[n]=T[n-1]+T[n-2].

Это легко проверить на последующих членах ряда.

Привлекательность рекурсивного вычисления заключается в том, что оно позволяет с помощью конечного высказывания определить бесконечное множество объектов. А конечной рекурсивной программой можно описать бесконечное число вычислений. Поэтому, подобно операторам цикла, рекурсивные процедуры управляются некоторым условием, нарушение которого приводит к завершению процедуры рекурсии.

Рекурсивные программы выполняются в виде процедур, или подпрограмм, и могут быть вызваны либо прямой ссылкой на себя, либо косвенно, через некоторую другую программу, содержащую рекурсию.

Широкое распространение получили рекуррентные (рекурсивные) алгоритмы, программная реализация которых отличается от реализации рекурсий, но эффективность которых не уступает рекурсивным процедурам.

В пособии не ставится цель показать эффективность программных решений алгоритмов, но с точки зрения вычислительных процедур необходимо привести ряд примеров.

Наиболее часто в качестве аппроксимирующей функции используется многочлен m-ой степени:

.

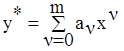Вычисления у* будут проведены за меньшое количество шагов, если воспользоваться схемой Горнера:

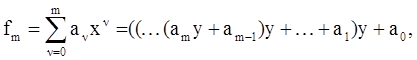
которая может быть описана рекуррентной процедурой:

1-й шаг: ;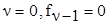

2-й шаг: ; ;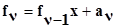

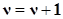3-й шаг: если 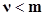, повторить 2-й шаг;

4-й шаг: вывод результата .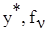

Рекурсию можно организовать не только по возрастанию порядка модели, как показано в примере, но также по увеличению числа рассматриваемых для этой модели переменных.

В этом плане достаточно просто вычисляются ортогональные полиномы, например, в виде следующей двухступенчатой рекуррентной процедуры:

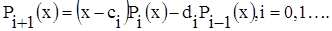(6.1)

При начальных значениях

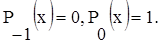
Коэффициенты с_i и d_i определяются из условия ортогональности

по следующим формулам:

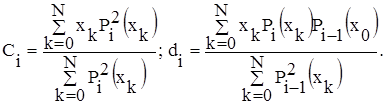(6.2)

Для i=0 в силу выше указанных выражений имеем

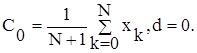
Поочередно используя формулы (6.1) и (6.2), можно определить полином любого порядка. Для многомерной функции процедуры (6.1) и (6.2) усложняются, но эффективность рекуррентной процедуры при этом возрастает.

Можно записать рекуррентное соотношение не только для вычисления аппроксимирующих функций, но и для оценивания остаточной суммы, для рекуррентного оценивания коэффициен­тов аппроксимирующих функций как линейных, так и нелинейных. В последнее время эти вопросы достаточно широко освещаются в литературе [5].

Дата добавления: 2014-08-04; просмотров: 378; Нарушение авторских прав

Мы поможем в написании ваших работ!